page 13
Note: the contents of this page as well as those which precede and follow, must be read as a continuation and/or overlap in order that the continuity about a relationship to/with the dichotomous arrangement of the idea that one could possibly talk seriously about peace from a different perspective as well as the typical dichotomous assignment of Artificial Intelligence (such as the usage of zeros and ones used in computer programming) ... will not be lost (such as war being frequently used to describe an absence of peace and vice-versa). However, if your mind is prone to being distracted by timed or untimed commercialization (such as that seen in various types of American-based television, radio, news media and magazine publishing... not to mention the average classroom which carries over into the everyday workplace), you may be unable to sustain prolonged exposures to divergent ideas about a singular topic without becoming confused, unless the information is provided in a very simplistic manner.
Let's face it, humanity has a lousy definition, accompanying practice, and analysis of peace.
In describing humanity's definition and practice of peace as something that is less than that to be desired, this does not mean that which is attempted is not wanted nor warranted. Nor does this mean the efforts of the Nobel Peace Prize Committee are without merit. We are simply trying to point out that the lack of a sustained peace means that we do not actually understand what is meant in order to bring about a sustained global peace. Whereas we may choose to claim that the lack of a sustained peace has more to do with the dynamics of human behavior in changing social climates that are no longer isolated from one another as they once were... preferring this or another interpretation instead of describing Peace as having a poor definition and practice; the situation remains is that we have not really thought about peace in terms of a global forum. The fact that we do not make the topic of peace a mandatory part of every single educational curriculum, speaks volumes of how much humanity takes the topic of peace for granted.
Conflict resolution is a topic assigned to advanced counseling instruction when it should be taught as a mandatory education course tailored to different grade levels. We are not taught as children to resolve conflicts with concepts directed towards developing a mindset to seek amicability amongst divergent positions. Instead, children (and adults) are subjected to television shows, music and adult activity involving fights, combativeness, arguments... and anything but resolving a situation except through violence, self-mutilation, suicide, drug involvement, alcohol, etc., or some "civilized" method involving kick-boxing, wrestling, sports aggression, etc... No less, on the flip-side, when people try to present "peaceful" programming, it typically involves situations that reflect occurrences of conflict resolution originating from being exposed to a violent world that does not actually define or practice a global interest in Peace.
Peace is being treated as an "Elective" course that only a few students take because there is no real graduating credit being given to it. Why in the world would anyone want to spend time on thinking about, much less practicing the topic of Peace, when the only upwardly mobile social reward is to receive a Nobel Peace Prize given only to a select few based on the criteria of a select few whose knowledge of Peace may be just as biased as world's interest in the topic? If you are not particularly intent on analyzing the phenomena we call Peace, you may be like most people who are unaware of the various peace organizations whose efforts typically are individualized with no inter-global effort. Most people may not be able to name a handful of organizations labeling themselves as a Peace organization, because such organizations are not widely visible... because humanity has no exuberant pride in peace. The topic of peace may come to mind and reach a social level of discussion only during a war... yet after a war has been played out for awhile and people have become tired of it as a journalistic form of entertainment.
When it comes to the topic of peace, humanity is a hypocrite. Humanity doesn't want peace unless there is a greater profit to be made off of it instead of conflict or disharmony. If an unhappy workforce is more productive than one experiencing peace defined as harmony, the intent will be to ensure the workforce remains unhappy. The same goes for a citizenry. If a greater or individualized profit can be made by keeping a public subdued to a relative state of poverty, the collected tax monies can be put to use elsewhere, or hoarded in a "community chest"... though politicians can claim that there is a deficit, when none actually exists. The idea of such is used to unsettle the public so that it can be more easily manipulated for one or another political gain to be made. The fact that it is neither a deficit nor a balanced budget should be looked at, but whether the needs of the people are being met. The deficit/balanced budget dichotomy does not invite the public to think in a third option related to establishing economic peace. Far too many are invested in a mentality focused on non-peaceful results because they have learned this is how they can best make a fortune within the social/governing structure as it is laid out... one in which the practice of an Actual Democracy is falsified.
All too often we pair the notion of "Peace" with an "Absence of war or conflict", though we might also pair it with words like disharmony, unhappiness, unhealthy, thirst, hunger/starvation, homelessness, joblessness, weakness, ignorance, etc... The point to make is that the recurrence of the typical "Absence of war or conflict" pairing presents us with an unsymmetrical form of symmetry. The "symmetry" portion refers to the similarity of occurrence and the "unsymmetrical" portion refers to dissimilarities. This same reference occurs in the human body and other presumed symmetries when we take a closer look beyond our generalities. Whereas on the previous page we provided an reference to symmetry in physics, let us now do the same for biology, noting that yet another seemingly pattern-of-four (instead of a 3-to-1 ratio) is being mentioned as a basic pattern... though the grammatical usage of the word "and" as a conjunction separates 3 from one (spherical, radial, biradial, and bilateral) is as well overlooked in mathematics when a comma is used to separate three (ones, tens, hundreds) from thousands, and is seen when we use three coins in vending machines (nickels, dimes, quarters) and some accommodate the usage of a 1 dollar (paper) bill. Another example is seen in the old British expression of "playing three to one", which references the two testicles and penis to one vagina. Other three-to-one references will be provided below.
Symmetry in Biology In biology, (symmetry refers to) the repetition of the parts in an animal or plant in an orderly fashion. Specifically, symmetry refers to a correspondence of body parts, in size, shape, and relative position, on opposite sides of a dividing line or distributed around a central point or axis. With the exception of radial symmetry, external form has little relation to internal anatomy, since animals of very different anatomical construction may have the same type of symmetry. Certain animals, particularly most sponges and the ameboid protozoans, lack symmetry, having either an irregular shape different for each individual or else one undergoing constant changes of form. The vast majority of animals, however, exhibit a definite symmetrical form. Four such patterns of symmetry occur among animals: spherical, radial, biradial, and bilateral. In spherical symmetry, illustrated only by the protozoan groups Radiolaria and Heliozoia, the body has the shape of a sphere and the parts are arranged concentrically around or radiate from the centre of the sphere. Such an animal has no ends or sides, and any plane passing through the centre will divide the animal into equivalent halves. The spherical type of symmetry is possible only in minute animals of simple internal construction, since in spheres the interior mass is large relative to the surface area and becomes too large for efficient functioning with increase in size and complexity. In radial symmetry the body has the general form of a short or long cylinder or bowl, with a central axis from which the body parts radiate or along which they are arranged in regular fashion. The main axis is heteropolar—i.e., with unlike ends, one of which bears the mouth and is termed the oral, or anterior, end, and the other of which, called the aboral, or posterior, end, forms the rear end of the animal and may bear the anus. The main axis is hence termed the oral-aboral, or anteroposterior, axis. Except in animals having an odd number of parts arranged in circular fashion (as in the five-armed starfishes), any plane passing through this axis will divide the animal into symmetrical halves. Animals having three, five, seven, etc., parts in a circle have symmetry that may be referred to, respectively, as three-rayed, five-rayed, seven-rayed, etc.; only certain planes through the axis will divide such animals into symmetrical halves. Radial symmetry is found in the coelenterates and echinoderms. In biradial symmetry, in addition to the anteroposterior axis, there are also two other axes or planes of symmetry at right angles to it and to each other: the sagittal, or median vertical-longitudinal, and transverse, or cross, axes. Such an animal therefore not only has two ends but also has two pairs of symmetrical sides. There are but two planes of symmetry in a biradial animal, one passing through the anteroposterior and sagittal axes and the other through the anteroposterior and transverse axes. Biradial symmetry occurs in the comb jellies. In bilateral symmetry there are the same three axes as in biradial symmetry but only one pair of symmetrical sides, the lateral sides, since the other two sides, called the dorsal (back) and ventral (belly) surfaces, are unlike. Thus, only one plane of symmetry will divide a bilateral animal into symmetrical halves, the median longitudinal, or sagittal, plane. Bilateral symmetry is characteristic of the vast majority of animals, including insects, fishes, amphibians, reptiles, birds, mammals, and most crustaceans. The concept of symmetry is also applied in botany. A flower is considered symmetrical when each whorl consists of an equal number of parts or when the parts of any one whorl are multiples of that preceding it. Thus, a symmetrical flower may have five sepals, five petals, five stamens, and five carpels, or the number of any of these parts may be a multiple of five.  The number of parts in the pistillate whorl is frequently not in conformity with that in the other whorls, but in such cases the flower is still called symmetrical, provided that the other whorls are normal. A flower in which the parts are in twos is dimerous; in threes, fours, or fives, (trimerous, tetramerous, or pentamerous), respectively. Trimerous symmetry is the rule in the monocotyledons, pentamerous the most common in the dicotyledons, although dimerous and tetramerous flowers also occur in the latter group.  When the different members of each whorl are alike, the flower is regular and is referred to as actinomorphic, or radially symmetrical, as in the petunia, buttercup, and wild rose. Differences in size or shape of the parts of a whorl make the flower irregular (as in the canna and Asiatic dayflower). When a flower can be divided by a single plane into two equal parts, it is zygomorphic, or bilaterally symmetrical, as in the snapdragon, orchid, and sweet pea.  Source: "Symmetry." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Note: just because someone says something lacks symmetry (as in the above comment about sponges), this only means they can't see any based on their typically used criteria. By altering one's definition, one can alter one's perception, while being cognizant of the fact that imagination can sometimes create illustrations that are specific to time and place and are not transferable using the same type of labeling. Transferring from one venue of perception to another an trying to find a regularity of patterning may require a larger, or newer definition that in retrospect, has taken one quite an intellectual distance from where they began... and still, the experts of your era may not be able to appreciate what your are proposing.
Here's a reference to symmetry in sponges located in a discussion about crystalline structures in skeletons, to which, because it came to mind... we can add the symmetry found in the skeletons of trees (note as tree rings in petrified wood); and a metaphorical comparison can be made to the topic of peace in that its unsustainability and thus inflexibility, is reminiscent of an articulated cognitive skeleton set off in the corner of most people's minds, like a wired-together prop of a human skeleton suspended off the floor on a roll-away support used in anatomy classes. Peace has become like so many calcified things except that it is not completely dead, just restrained like someone felt to be non-normal, and let out of their room or hospital every now and then to get a breath of fresh air. We treat peace like an invalid, like an infant, like a child, like an adolescent that must be held under house arrest called being grounded (which, by the way is an old air force — military — reference), but never treated as an adult; because humanity has not grown up enough to understand the true personality of peace. Humanity does not want Peace to run free, nor experience a full-fledged Democratic way of life. Like an over-protective parent who wants to control peace and develop institutions which will provide a few with social recognition and perhaps some financial reward, humanity does not want peace to walk freely amongst the world as a sovereign identity unto its own. Business wants to control peace. Government wants to control peace. Religion wants to control peace. And even "mother" earth wants to bind peace to her apron strings if it can not bind humanity with an umbilical cord to keep it from seeking its own way in the larger Universe. Peace must be set free, just as the people must be set free by experiencing the path named an Actual Democracy. Set Us Free!
Crystals Crystals form the basis of many skeletons, such as the calcareous triradiate (three-armed) and quadradiate (four-armed) spicules of calcareous sponges. The cellular components of the body of the sponge usually are not rigid and have no fixed continuity; cells from the outer, inner, and middle layers of a sponge are freely mobile. Spicules, which may be of silica, often extend far from the body. They can be shed at times and replaced by new spicules. Skeletal fibres are present in many sponges. Calcareous spicules, large and small, form an important part of the skeleton of many coelenterates. Huge needlelike spicules, projecting beyond the soft tissue of sea pens (pennatulids), for example, both support the flanges that bear feeding polyps and hinder browsing by predators. Minute internal spicules may be jammed together to form a skeletal axis, as in the red coral. In some corals (Alcyonaria), spicules combine with fibres made of keratin (a protein also found in hair and feathers) or keratins with amorphous calcite (noncrystalline calcium carbonate) to form axial structures of great strength and size, enabling colonies to reach large bushlike proportions. Skeletons consisting of cuticle but remote from the body surface give support and protection to other coelenterates, the colonial sedentary hydroids, and form tubes in which pogonophores (small threadlike aquatic animals) live. Exoskeletons that are superficially similar but quite different from hydroids and pogonophores in both manner of growth and internal support occur in the graptolites, an extinct group, and in the protochordates, Rhabdopleura and Cephalodiscus. Some graptolites, known only from fossil skeletal remains many millions of years old, had skeletons similar to those of Rhabdopleura. In segmented and in many nonsegmented invertebrates, cuticle is secreted by the ectoderm and remains in contact with it. It is thin in annelid worms (e.g., the earthworm) and thicker in roundworms (nematodes) and arthropods. In many arthropods the cuticle is infolded to form endoskeletal structures of considerable complexity. Rigidity is imposed on parts of the cuticle of arthropods either by sclerotization or tanning, a process involving dehydration (as in crustaceans and insects), by calcification (as in millipedes), or by both, as in many crabs. In most arthropods the body and legs are clearly segmented. On the dorsal (upper) side of each segment is a so-called tergal sclerite of calcified or sclerotized cuticle, usually a ventral (lower) sternite and often lateral pleurites—i.e., side plates. There may be much fusion of sclerites on the same segment. Sometimes fusion occurs between dorsal sclerites of successive segments, to form rigid plates. Leg sclerotizations are usually cylindrical. Internally, apodemes are hollow rods or flanges derived from the cuticle; they extend inward from the exoskeleton. Apodemes have a function similar to the bones of vertebrates, for they provide sites for muscle insertion, thereby allowing the leverage that can cause movement of other parts of the skeleton independent of hydrostatic forces. The apodemal system is most fully developed in the larger and more swiftly moving arthropods. The cuticle is a dead secretion and can only increase in thickness. At intervals an arthropod molts the entire cuticle, pulling out the apodemes. The soft body rapidly swells before secreting a new, stiff cuticle. The molting process limits the upper size of cuticle-bearing animals. Arthropods can never achieve the body size of the larger vertebrates, in which the bones grow with the body, because the mechanical difficulties of molting would be too great. The mechanical properties of bone limit terrestrial mammals to about the size of a 12-ton elephant. In water, however, bone can support a heavier animal, such as a blue whale weighing 100 tons. Bone is mechanically unsuited to support an animal as bulky as, for example, a large ship. Semirigid structures Flexible cuticular structures on the surface of unsegmented roundworms and arthropods are just as important in providing support as are the more rigid sclerites. Mobility between the sclerites of body and legs is maintained by regions of flexible cuticle, the arthrodial membranes. Some sclerites are stiffened by closely packed cones of sclerotization at their margins, forming structures that combine rigidity and flexibility. |
As can be noted, the usage of Peace is rather rigid and not very flexible, or it many variations would be extant throughout the world like a diversity of species. However, humanity's mentality, due to an ongoing conservation of pattern usage, is particularly solidified in it perceptions against peace being as a living entity with full rights and privileges. Whereas humanity gives businesses a distinction of "personhood"— peace, freedom, liberty, justice and democracy are not to share in such a distinction with equal merit. Business, government and religion are much too selfish to permit such. Additionally, let us note that an environment with a different gravity who enable different uses of skeletal arrangements... either disallowing large vertebrates or providing assistance to very large bodied ones.
Now let's take a look at symmetry in crystallography that uses different criteria to identify a definition:
Symmetry in Crystallography In crystallography, (symmetry is the) fundamental property of the orderly arrangements of atoms found in crystalline solids. Each arrangement of atoms has a certain number of elements of symmetry; i.e., changes in the orientation of the arrangement of atoms seem to leave the atoms unmoved. One such element of symmetry is rotation; other elements are translation, reflection, and inversion. The elements of symmetry present in a particular crystalline solid determine its shape and affect its physical properties. Translations involve displacement of the crystal in a direction that replaces each atom by one of its identical neighbours, so that the atoms seem unmoved. Rotations turn the crystal around an axis of symmetry passing through the crystal; the only rotations compatible with translational symmetry move the crystal through an angle of 360° divided by n, with n equal to 1, 2, 3, 4, or 6. Reflections exchange the parts of the crystal on the two sides of a plane of symmetry (mirror plane) within the solid. Inversions move every atom to another position in the crystal; the old and new positions of the atom lie upon a line, at the middle of which is the centre of inversion. So-called improper rotations are rotations followed by reflections (known as roto-reflections) or rotations followed by inversions (called rotoinversions). A crystal can be classified according to its elements of symmetry; for example, it may belong to one of 230 space groups, 32 point groups, 14 Bravais lattices, and 7 crystal systems. A crystal can be represented diagrammatically by an orderly stacking of unit cells; the shape of the unit cell determines which of the seven crystal systems the crystal belongs to. Unit cells of the same shape may have points (each representing an atom or a group of atoms) at their centres or on their faces, in addition to those at their corners. These additional lattice points divide the 7 crystal systems into 14 Bravais lattices; the Bravais lattices are subdivided into 32 crystal classes, or point groups. Each point group corresponds to one of the possible combinations of rotations, reflections, inversions, and improper rotations; with the inclusion of translational elements, 230 space groups are produced. Source: "Symmetry." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Peace, as it is defined and applied, takes on a repetitive... a conserved expression... as if humanity is caught in a hamster wheel that is slowing down and the hamster must make physiological, mental and emotional adjustments to the deterioration even though it may not be conscious of the incremental deterioration.
With respect to crystals used as an example of symmetry in which we are pairing a discussion of Peace with, and because we note that there is an intermittancy, or irregularity (and thus unsustainability) to peace, a look at the phenomena of quasi-crystals is of relevance, because "Peace" is a phenomena we do not yet comprehend and as result, create fanciful notions, ceremonies and activities regarding it. Peace is the result of two different structures (peace/war) set into the frame work of a mentality using a three-patterned array (as seen in the various three-patterned examples already provided):
Quasi-Crystal (also called quasi-periodic crystal) (Quasicrystal is) matter formed atomically in a manner somewhere between the amorphous solids of glasses (special forms of metals and other minerals, as well as common glass) and the precise pattern of crystals. Like crystals, quasicrystals contain an ordered structure, but the patterns are subtle and do not recur at precisely regular intervals. Rather, quasicrystals appear to be formed from two different structures assembled in a non-repeating array, the three-dimensional equivalent of a tile floor made from two shapes of tile and having an orientational order but no repetition. Although when first discovered such structures surprised the scientific community, it now appears that quasicrystals rank among the most common structures in alloys of aluminum with such metals as iron, cobalt, or nickel. While no major commercial applications yet exploit properties of the quasicrystalline state directly, quasicrystals form in compounds noted for their high strength and light weight, suggesting potential applications in aerospace and other industries. Michael Widom: Professor of Physics, Carnegie Mellon University, Pittsburgh, Pennsylvania. Author of Renormalization Group Analysis of Quasi-Periodicity in Analytic Maps.Source: "Quasicrystal." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
If peace is an as yet unidentified entity given a wrong label, its better application may not be used for other applications. For example, let us say that the notion of peace is a hint, an echo, a reverberation of a pebble dropped in a pool of water... but we can only see a portion of the concentric waves. We need see the size of the pool of water, the object from which the waves emanate, or that our language inclinations are guided by underlying mental patterns that are conserved and being subjected to a deteriorating environment. This then explains, in a metaphorical sense, why peace is wrongly understood... despite all the social pageantry we apply to it. The on again/off again emergence of relative peace seems rather circular-like, that may be better described as a helical structure as the following two images illustrate. The irregularity of Peace can be viewed in an historical-time related sense thus introducing the concept of time as being less a straight arrow, but a wobbly one going in a direction that may be altered and thus deflect time (with respect to human existence) along (unmarked?/"natural") paths, trails or "corridors" now being described as a multi-dimension possibility:
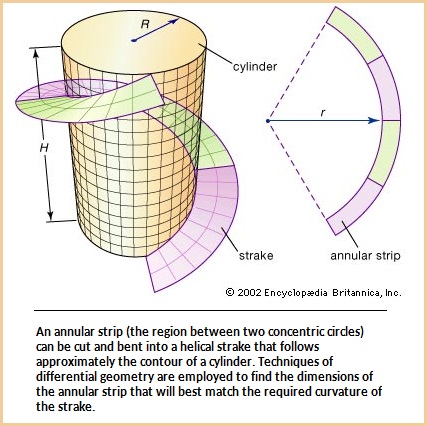 |
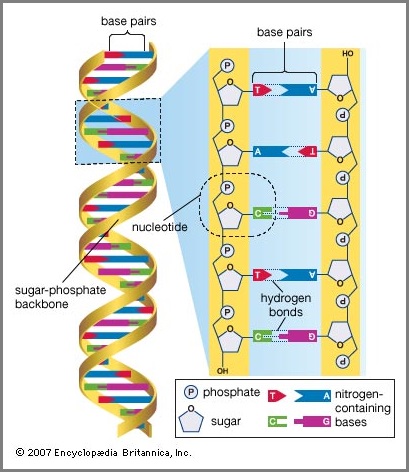 |
 |
|
Date of Origination: Wednesday, 21-Dec-2016... 03:52 AM
Date of initial posting: Wednesday, 21-Dec-2016...10:31 AM
Updated posting: Saturday, 31-March-2018... 11:39 AM