Declaration For Greater Independence

Symmetry

• In Brain Hemispheres: Let's Talk Peace page 11
• In Physics: Let's Talk Peace page 12
• In Biology and Crystallography: Let's Talk Peace page 13
• In Early Organisms: Let's Talk Peace page 30
• As an expression denoted as parity: Let's Talk Peace page 48

Symmetry in "Principles of Physical Science"

The normal behaviour of a gas on cooling is to condense into a liquid and then into a solid, though the liquid phase may be left out if the gas starts at a low enough pressure. The solid phase of a pure substance is usually crystalline, having the atoms or molecules arranged in a regular pattern so that a suitable small sample may define the whole. The unit cell is the smallest block out of which the pattern can be formed by stacking replicas. The checkerboard in Figure 12 illustrates the idea; here the unit cell has been chosen out of many possibilities to contain one white square and one black, dissected into quarters. For crystals, of course, the unit cell is three-dimensional. A very wide variety of arrangements is exhibited by different substances, and it is the great triumph of X-ray crystallography to have provided the means for determining experimentally what arrangement is involved in each case.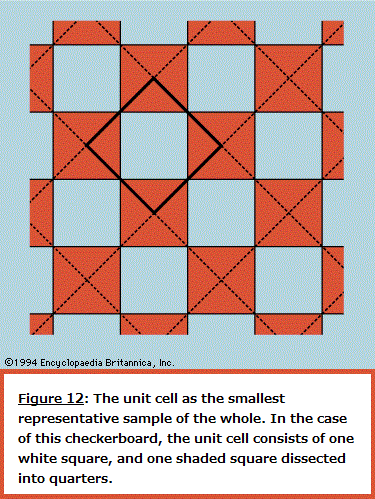

One may ask whether mathematical techniques exist for deducing the correct result independently of experiment, and the answer is almost always no. An individual sulfur atom, for example, has no features that reflect its preference, in the company of others, for forming rings of eight. This characteristic can only be discovered theoretically by calculating the total energy of different-sized rings and of other patterns and determining after much computation that the ring of eight has the lowest energy of all. Even then the investigator has no assurance that there is no other arrangement which confers still lower energy. In one of the forms taken by solid sulfur, the unit cell contains 128 atoms in a complex of rings. It would be an inspired guess to hit on this fact without the aid of X-rays or the expertise of chemists, and mathematics provides no systematic procedure as an alternative to guessing or relying on experiment.

Nevertheless, it may be possible in simpler cases to show that calculations of the energy are in accord with the observed crystal forms. Thus, when silicon is strongly compressed, it passes through a succession of different crystal modifications for each of which the variation with pressure of the energy can be calculated. The pressure at which a given change of crystal form takes place is that at which the energy takes the same value for both modifications involved. As this pressure is reached, one gives way to the other for the possession of the lower energy. The fact that the calculation correctly describes not only the order in which the different forms occur but also the pressures at which the change-overs take place indicates that the physical theory is in good shape; only the power is lacking in the mathematics to predict behaviour from first principles.

The changes in symmetry that occur at the critical points where one modification changes to another are complex examples of a widespread phenomenon for which simple analogues exist. A perfectly straight metal strip, firmly fixed to a base so that it stands perfectly upright, remains straight as an increasing load is placed on its upper end until a critical load is reached. Any further load causes the strip to heel over and assume a bent form, and it only takes a minute disturbance to determine whether it will bend to the left or to the right. The fact that either outcome is equally likely reflects the left–right symmetry of the arrangement, but once the choice is made the symmetry is broken. The subsequent response to changing load and the small vibrations executed when the strip is struck lightly are characteristic of the new unsymmetrical shape. If one wishes to calculate the behaviour, it is essential to avoid assuming that an arrangement will always remain symmetrical simply because it was initially so. In general, as with the condensation of sulfur atoms or with the crystalline transitions in silicon, the symmetry implicit in the formulation of the theory will be maintained only in the totality of possible solutions, not necessarily in the particular solution that appears in practice. In the case of the condensation of a crystal from individual atoms, the spherical symmetry of each atom tells one no more than that the crystal may be formed equally well with its axis pointing in any direction; and such information provides no help in finding the crystal structure. In general, there is no substitute for experiment. Even with relatively simple systems such as engineering structures, it is all too easy to overlook the possibility of symmetry breaking, leading to calamitous failure.

It should not be assumed that the critical behaviour of a loaded strip depends on its being perfectly straight. If the strip is not, it is likely to prefer one direction of bending to the other. As the load is increased, so will the intrinsic bend be exaggerated, and there will be no critical point at which a sudden change occurs. By tilting the base, however, it is possible to compensate for the initial imperfection and to find once more a position where left and right are equally favoured. Then the critical behaviour is restored, and at a certain load the necessity of choice is present as with a perfect strip. The study of this and numerous more complex examples is the province of the so-called catastrophe theory. A catastrophe, in the special sense used here, is a situation in which a continuously varying input to a system gives rise to a discontinuous change in the response at a critical point. The discontinuities may take many forms, and their character may be sensitive in different ways to small changes in the parameters of the system. Catastrophe theory is the term used to describe the systematic classification, by means of topological mathematics, of these discontinuities. Wide-ranging though the theory may be, it cannot at present include in its scope most of the symmetry-breaking transitions undergone by crystals.

Entropy and disorder

As is explained in detail in the article thermodynamics, the laws of thermodynamics make possible the characterization of a given sample of matter—after it has settled down to equilibrium with all parts at the same temperature—by ascribing numerical measures to a small number of properties (pressure, volume, energy, and so forth). One of these is entropy. As the temperature of the body is raised by adding heat, its entropy as well as its energy is increased. On the other hand, when a volume of gas enclosed in an insulated cylinder is compressed by pushing on the piston, the energy in the gas increases while the entropy stays the same or, usually, increases a little. In atomic terms, the total energy is the sum of all the kinetic and potential energies of the atoms, and the entropy, it is commonly asserted, is a measure of the disorderly state of the constituent atoms. The heating of a crystalline solid until it melts and then vaporizes is a progress from a well-ordered, low-entropy state to a disordered, high-entropy state. The principal deduction from the second law of thermodynamics (or, as some prefer, the actual statement of the law) is that, when an isolated system makes a transition from one state to another, its entropy can never decrease. If a beaker of water with a lump of sodium on a shelf above it is sealed in a thermally insulated container and the sodium is then shaken off the shelf, the system, after a period of great agitation, subsides to a new state in which the beaker contains hot sodium hydroxide solution. The entropy of the resulting state is higher than the initial state, as can be demonstrated quantitatively by suitable measurements.

The idea that a system cannot spontaneously become better ordered but can readily become more disordered, even if left to itself, appeals to one's experience of domestic economy and confers plausibility on the law of increase of entropy. As far as it goes, there is much truth in this naive view of things, but it cannot be pursued beyond this point without a much more precise definition of disorder. Thermodynamic entropy is a numerical measure that can be assigned to a given body by experiment; unless disorder can be defined with equal precision, the relation between the two remains too vague to serve as a basis for deduction. A precise definition is to be found by considering the number, labeled W, of different arrangements that can be taken up by a given collection of atoms, subject to their total energy being fixed. In quantum mechanics, W is the number of different quantum states that are available to the atoms with this total energy (strictly, in a very narrow range of energies). It is so vast for objects of everyday size as to be beyond visualization; for the helium atoms contained in one cubic centimetre of gas at atmospheric pressure and at 0°C the number of different quantum states can be written as 1 followed by 170 million million million zeroes (written out, the zeroes would fill nearly one trillion sets of the Encyclopædia Britannica).

The science of statistical mechanics, as founded by Ludwig Boltzmann and J. Willard Gibbs, relates the behaviour of a multitude of atoms to the thermal properties of the material they constitute. Boltzmann and Gibbs, along with Max Planck, established that the entropy, S, as derived through the second law of thermodynamics, is related to W by the formula S = k ln W, where k is the Boltzmann constant (1.3806488 x 10^-23 joule per kelvin) and ln W is the natural (Naperian) logarithm of W. By means of this and related formulas it is possible in principle, starting with the quantum mechanics of the constituent atoms, to calculate the measurable thermal properties of the material. Unfortunately, there are rather few systems for which the quantum mechanical problems succumb to mathematical analysis, but among these are gases and many solids, enough to validate the theoretical procedures linking laboratory observations to atomic constitution.

When a gas is thermally isolated and slowly compressed, the individual quantum states change their character and become mixed together, but the total number W does not alter. In this change, called adiabatic, entropy remains constant. On the other hand, if a vessel is divided by a partition, one side of which is filled with gas while the other side is evacuated, piercing the partition to allow the gas to spread throughout the vessel greatly increases the number of states available so that W and the entropy rise. The act of piercing requires little effort and may even happen spontaneously through corrosion. To reverse the process, waiting for the gas to accumulate accidentally on one side and then stopping the leak, would mean waiting for a time compared with which the age of the universe would be imperceptibly short. The chance of finding an observable decrease in entropy for an isolated system can be ruled out.

This does not mean that a part of a system may not decrease in entropy at the expense of at least as great an increase in the rest of the system. Such processes are indeed commonplace but only when the system as a whole is not in thermal equilibrium. Whenever the atmosphere becomes supersaturated with water and condenses into a cloud, the entropy per molecule of water in the droplets is less than it was prior to condensation. The remaining atmosphere is slightly warmed and has a higher entropy. The spontaneous appearance of order is especially obvious when the water vapour condenses into snow crystals. A domestic refrigerator lowers the entropy of its contents while increasing that of its surroundings. Most important of all, the state of non-equilibrium of the Earth irradiated by the much hotter Sun provides an environment in which the cells of plants and animals may build order—i.e., lower their local entropy at the expense of their environment. The Sun provides a motive power that is analogous (though much more complex in detailed operation) to the electric cable connected to the refrigerator. There is no evidence pointing to any ability on the part of living matter to run counter to the principle of increasing (overall) disorder as formulated in the second law of thermodynamics.

The irreversible tendency toward disorder provides a sense of direction for time which is absent from space. One may traverse a path between two points in space without feeling that the reverse journey is forbidden by physical laws. The same is not true for time travel, and yet the equations of motion, whether in Newtonian or quantum mechanics, have no such built-in irreversibility. A motion picture of a large number of particles interacting with one another looks equally plausible whether run forward or backward. To illustrate and resolve this paradox it is convenient to return to the example of a gas enclosed in a vessel divided by a pierced partition. This time, however, only 100 atoms are involved (not 3 x 10¹⁹ as in one cubic centimetre of helium), and the hole is made so small that atoms pass through only rarely and no more than one at a time. This model is easily simulated on a computer, and Figure 13 shows a typical sequence during which there are 500 transfers of atoms across the partition. The number on one side starts at the mean of 50 and fluctuates randomly while not deviating greatly from the mean. Where the fluctuations are larger than usual, as indicated by the arrows, there is no systematic tendency for their growth to the peak to differ in form from the decay from it. This is in accord with the reversibility of the motions when examined in detail.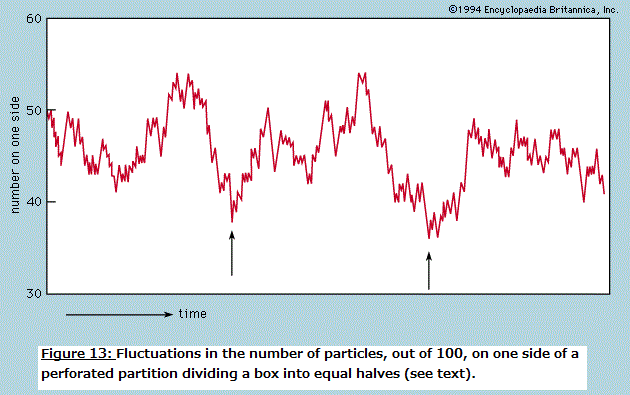

If one were to follow the fluctuations for a very long time and single out those rare occasions when a particular number occurred that was considerably greater than 50, say 75, one would find that the next number is more likely to be 74 than 76. Such would be the case because, if there are 75 atoms on one side of the partition, there will be only 25 on the other, and it is three times more likely that one atom will leave the 75 than that one will be gained from the 25. Also, since the detailed motions are reversible, it is three times more likely that the 75 was preceded by a 74 rather than by a 76. In other words, if one finds the system in a state that is far from the mean, it is highly probable that the system has just managed to get there and is on the point of falling back. If the system has momentarily fluctuated into a state of lower entropy, the entropy will be found to increase again immediately.

It might be thought that this argument has already conceded the possibility of entropy decreasing. It has indeed, but only for a system on the minute scale of 100 atoms. The same computation carried out for 3 x 10¹⁹ atoms would show that one would have to wait interminably (i.e., enormously longer than the age of the universe) for the number on one side to fluctuate even by as little as one part per million. A physical system as big as the Earth, let alone the entire Galaxy—if set up in thermodynamic equilibrium and given unending time in which to evolve—might eventually have suffered such a huge fluctuation that the condition known today could have come about spontaneously. In that case man would find himself, as he does, in a universe of increasing entropy as the fluctuation recedes. Boltzmann, it seems, was prepared to take this argument seriously on the grounds that sentient creatures could only appear as the aftermath of a large enough fluctuation. What happened during the inconceivably prolonged waiting period is irrelevant. Modern cosmology shows, however, that the universe is ordered on a scale enormously greater than is needed for living creatures to evolve, and Boltzmann's hypothesis is correspondingly rendered improbable in the highest degree. Whatever started the universe in a state from which it could evolve with an increase of entropy, it was not a simple fluctuation from equilibrium. The sensation of time's arrow is thus referred back to the creation of the universe, an act that lies beyond the scrutiny of the physical scientist.

t is possible, however, that in the course of time the universe will suffer "heat death," having attained a condition of maximum entropy, after which tiny fluctuations are all that will happen. If so, these will be reversible, like the graph of Figure 13, and will give no indication of a direction of time. Yet, because this undifferentiated cosmic soup will be devoid of structures necessary for consciousness, the sense of time will in any case have vanished long since.

Chaos

Many systems can be described in terms of a small number of parameters and behave in a highly predictable manner. Were this not the case, the laws of physics might never have been elucidated. If one maintains the swing of a pendulum by tapping it at regular intervals, say once per swing, it will eventually settle down to a regular oscillation. Now let it be jolted out of its regularity; in due course it will revert to its previous oscillation as if nothing had disturbed it. Systems that respond in this well-behaved manner have been studied extensively and have frequently been taken to define the norm, from which departures are somewhat unusual. It is with such departures that this section is concerned.

An example not unlike the periodically struck pendulum is provided by a ball bouncing repeatedly in a vertical line on a base plate that is caused to vibrate up and down to counteract dissipation and maintain the bounce. With a small but sufficient amplitude of base motion the ball synchronizes with the plate, returning regularly once per cycle of vibration. With larger amplitudes the ball bounces higher but still manages to remain synchronized until eventually this becomes impossible. Two alternatives may then occur: (1) the ball may switch to a new synchronized mode in which it bounces so much higher that it returns only every two, three, or more cycles, or (2) it may become unsynchronized and return at irregular, apparently random, intervals. Yet, the behaviour is not random in the way that raindrops strike a small area of surface at irregular intervals. The arrival of a raindrop allows one to make no prediction of when the next will arrive; the best one can hope for is a statement that there is half a chance that the next will arrive before the lapse of a certain time. By contrast, the bouncing ball is described by a rather simple set of differential equations that can be solved to predict without fail when the next bounce will occur and how fast the ball will be moving on impact, given the time of the last bounce and the speed of that impact. In other words, the system is precisely determinate, yet to the casual observer it is devoid of regularity. Systems that are determinate but irregular in this sense are called chaotic; like so many other scientific terms, this is a technical expression that bears no necessary relation to the word's common usage.

The coexistence of irregularity with strict determinism can be illustrated by an arithmetic example, one that lay behind some of the more fruitful early work in the study of chaos, particularly by the physicist Mitchell J. Feigenbaum following an inspiring exposition by Robert M. May. Suppose one constructs a sequence of numbers starting with an arbitrarily chosen x₀ (between 0 and 1) and writes the next in the sequence, x₁, as Ax₀(1 - x₀); proceeding in the same way to x₂ = Ax₁(1 - x₁), one can continue indefinitely, and the sequence is completely determined by the initial value x₀ and the value chosen for A. Thus, starting from x₀ = 0.9 with A = 2, the sequence rapidly settles to a constant value: 0.09, 0.18, 0.2952, 0.4161, 0.4859, 0.4996, 0.5000, 0.5000, and so forth.

When A lies between 2 and 3, it also settles to a constant but takes longer to do so. It is when A is increased above 3 that the sequence shows more unexpected features. At first, until A reaches 3.42, the final pattern is an alternation of two numbers, but with further small increments of A it changes to a cycle of 4, followed by 8, 16, and so forth at ever-closer intervals of A. By the time A reaches 3.57, the length of the cycle has grown beyond bounds—it shows no periodicity however long one continues the sequence. This is the most elementary example of chaos, but it is easy to construct other formulas for generating number sequences that can be studied rapidly with the aid of the smallest programmable computer. By such "experimental arithmetic" Feigenbaum found that the transition from regular convergence through cycles of 2, 4, 8, and so forth to chaotic sequences followed strikingly similar courses for all, and he gave an explanation that involved great subtlety of argument and was almost rigorous enough for pure mathematicians.

The chaotic sequence shares with the chaotic bouncing of the ball in the earlier example the property of limited predictability, as distinct from the strong predictability of the periodically driven pendulum and of the regular sequence found when A is less than 3. Just as the pendulum, having been disturbed, eventually settles back to its original routine, so the regular sequence, for a given choice of A, settles to the same final number whatever initial value x₀ may be chosen. By contrast, when A is large enough to generate chaos, the smallest change in x₀ leads eventually to a completely different sequence, and the smallest disturbance to the bouncing ball switches it to a different but equally chaotic pattern. This is illustrated for the number sequence in Figure 14, where two sequences are plotted (successive points being joined by straight lines) for A = 3.7 and x₀ chosen to be 0.9 and 0.9000009, a difference of one part per million. For the first 35 terms the sequences differ by too little to appear on the graph, but a record of the numbers themselves shows them diverging steadily until by the 40th term the sequences are unrelated. Although the sequence is completely determined by the first term, one cannot predict its behaviour for any considerable number of terms without extremely precise knowledge of the first term. The initial divergence of the two sequences is roughly exponential, each pair of terms being different by an amount greater than that of the preceding pair by a roughly constant factor. Put another way, to predict the sequence in this particular case out to n terms, one must know the value of x₀ to better than n/8 places of decimals. If this were the record of a chaotic physical system (e.g., the bouncing ball), the initial state would be determined by measurement with an accuracy of perhaps 1 percent (i.e., two decimal places), and prediction would be valueless beyond 16 terms. Different systems, of course, have different measures of their "horizon of predictability," but all chaotic systems share the property that every extra place of decimals in one's knowledge of the starting point only pushes the horizon a small extra distance away. In practical terms, the horizon of predictability is an impassible barrier. Even if it is possible to determine the initial conditions with extremely high precision, every physical system is susceptible to random disturbances from outside that grow exponentially in a chaotic situation until they have swamped any initial prediction. It is highly probable that atmospheric movements, governed by well-defined equations, are in a state of chaos. If so, there can be little hope of extending indefinitely the range of weather forecasting except in the most general terms. There are clearly certain features of climate, such as annual cycles of temperature and rainfall, which are exempt from the ravages of chaos. Other large-scale processes may still allow long-range prediction, but the more detail one asks for in a forecast, the sooner will it lose its validity.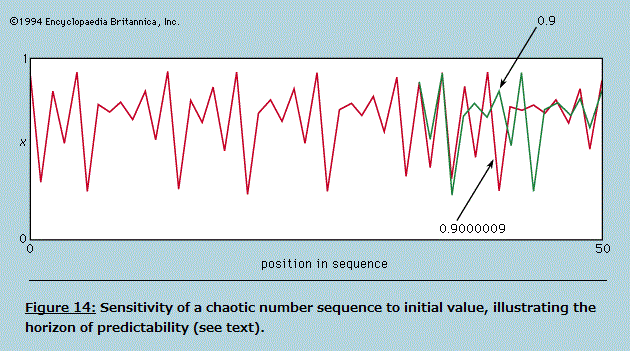

Linear systems for which the response to a force is strictly proportional to the magnitude of the force do not show chaotic behaviour. The pendulum, if not too far from the vertical, is a linear system, as are electrical circuits containing resistors that obey Ohm's law or capacitors and inductors for which voltage and current also are proportional. The analysis of linear systems is a well-established technique that plays an important part in the education of a physicist. It is relatively easy to teach, since the range of behaviour exhibited is small and can be encapsulated in a few general rules. Nonlinear systems, on the other hand, are bewilderingly versatile in their modes of behaviour and are, moreover, very commonly unamenable to elegant mathematical analysis. Until large computers became readily available, the natural history of nonlinear systems was little explored and the extraordinary prevalence of chaos unappreciated. To a considerable degree physicists have been persuaded, in their innocence, that predictability is a characteristic of a well-established theoretical structure; given the equations defining a system, it is only a matter of computation to determine how it will behave. However, once it becomes clear how many systems are sufficiently nonlinear to be considered for chaos, it has to be recognized that prediction may be limited to short stretches set by the horizon of predictability. Full comprehension is not to be achieved by establishing firm fundamentals, important though they are, but must frequently remain a tentative process, a step at a time, with frequent recourse to experiment and observation in the event that prediction and reality have diverged too far.