Declaration For Greater Independence

Tuning and Temperament

Introduction

In music, (tuning and temperament is) the adjustment of one sound source, such as a voice or string, to produce a desired pitch in relation to a given pitch, and the modification of that tuning to lessen dissonance. The determination of pitch, the quality of sound that is described as "high" or "low," is based upon the frequency of sound waves.

Two concepts fundamental to the theory of tuning are those of frequency ratio and of consonance and dissonance. A given musical pitch is determined by the frequency of vibration of the sound wave that produces it, as a' = 440 cycles per second. An interval, or distance between two pitches, can thus be mathematically described as the ratio of the frequency of the first pitch to the frequency of the second. Various frequency ratios can be reduced to the same basic relationship; for example, 440:220 and 30:15 and 750:375 can all be reduced to the ratio 2:1.

When two tones are sounded together the subjective reaction may be anything from one of perfect consonance to one of extreme dissonance. Dissonance is produced by beats (interference between pulsations of sound waves), and it is found that maximum dissonance occurs when the rate of beats between the two tones is about 33 per second. Consonance results from the absence of beats, which occurs only when the ratio between the frequencies of the two tones is numerically simple. When the two tones are tuned to the same pitch, they are said to be in unison (ratio 1:1) and their consonance is absolute. Next in order of consonance comes the octave (2:1), the interval between c and c' (encompassing eight notes of the piano keyboard); another highly consonant interval is the fifth (3:2, as from c to g). When a unison, octave, or fifth is slightly mistuned, the resulting combination is markedly dissonant and is judged "out of tune." The slight mistunings that occur in systems of tempered tuning are necessary for reasons that will be discussed later in this article.

The problems of tuning

So long as music consists of melody without harmony, consonance plays little part in the determination of successive pitches in a scale. Many primitive scales are sung, not played, and are variable in the exact pitches of their notes. When instruments are made, it is often necessary to determine precise pitches. The tendency is either to make the steps in the scale sound equal in size or to place them in simple arithmetic relationship to one another. The fundamental unit is the octave, which has the unique property that its two notes are felt in some indefinable way to be the same, though in pitch level they are recognizably different. For this reason, high and low voices naturally sing the same tune an octave apart. In nearly all musical cultures the octave is subdivided into a number of steps, each a simple fraction of an octave. In the diatonic, or seven-note scale, for example, which is the basis of Western music and is represented by the white notes on the piano keyboard, there are five steps of one-sixth of an octave and two of one-twelfth. In contrast to these uncomplicated fractions, the frequency ratios of these intervals are actually the irrational numbers: ⁶ʃ2:1 and ¹²ʃ2:1. As has been noted, consonance is related to simple frequency ratios such as 2:1. Consequently, the arithmetic subdivision of the octave can never produce perfectly consonant intervals. This unavoidable fact underlies many of the problems in the history of tuning. Insignificant when notes are heard melodically, it becomes highly important when notes of different pitch are heard simultaneously. The complex development of harmony has been the most striking peculiarity of Western music, and it has brought with it a host of tuning problems.

Apart from the octave, which presents no problem, there are really only three distinct intervals in the diatonic scale the consonance of which is important. These are the fifth (3:2, as C-G), the major third (5:4, as C-E), and the major sixth (5:3, as C-A). The other three consonant intervals are the fourth (4:3, as C-F), the minor sixth (8:5, as C-A♭), and the minor third (6:5, as C-E♭). The intervals of this second group are not truly distinct, for they can be derived from the first three by inversion—i.e., by transposing the lower note of the interval up an octave. Thus, inverting the fifth c-g yields the fourth g-c'. Inverting the major third c-e yields the minor sixth e-c', and inverting the major sixth c-a yields the minor third a–c'. Because of the phenomenon of inversion, if the fifths in a scale are in tune, the fourths also will be in tune. For each of these six intervals the tuning expressed by the above simple frequency ratios sounds "right"; if modified slightly in either direction it sounds seriously out of tune. The same cannot be said of other intervals of the diatonic scale. The major and minor seventh (as c-b and d-c') and the diminished fifth (as b-f'), with their inversions, sound dissonant in any case; they have no one tuning that is clearly more acceptable than another. Hence the harmonic merits of any tuning system depend on the way fifths, major thirds, and major sixths are tuned. In the diatonic scale (indefinitely extended through several octaves) there are six perfect fifths (F-C, C-G, G-D, D-A, A-E, E-B), three major thirds (F-A, C-E, G-B), and four major sixths (F-D, C-A, G-E, D-B). It is impossible to tune the seven notes of the scale so that each of these 13 intervals is maximally consonant. This is the second inescapable obstacle to perfection in the tuning of the diatonic scale.

Classic tuning systems

Of the two ancient Greek systems that were used chiefly in the Middle Ages, one, Pythagorean tuning, makes all the fifths perfectly consonant. As a result, all the major thirds and major sixths are sharp (too wide) by 22 cents (a cent is 1/1200 of an octave) or by the ratio of 81:80. This amount is called a comma of Didymus, and it makes intervals severely dissonant when their notes are sounded simultaneously. Within the gamut, the pitch range in use during the Middle Ages, a major third or sixth mistuned by a comma beats between 6 and 32 times a second. Melodically, the Pythagorean system is satisfactory. (Table 1 compares whole tone and semitone sizes in the four main tuning systems.) Pythagorean tuning makes all five whole tones (the larger steps in the diatonic scale) equal at 9:8 (204 cents), and the two semitones (the smaller steps) equal at 256:243 ( 90 cents). The semitones are considerably less than half the whole tones in size, but this is not particularly objectionable in a melody.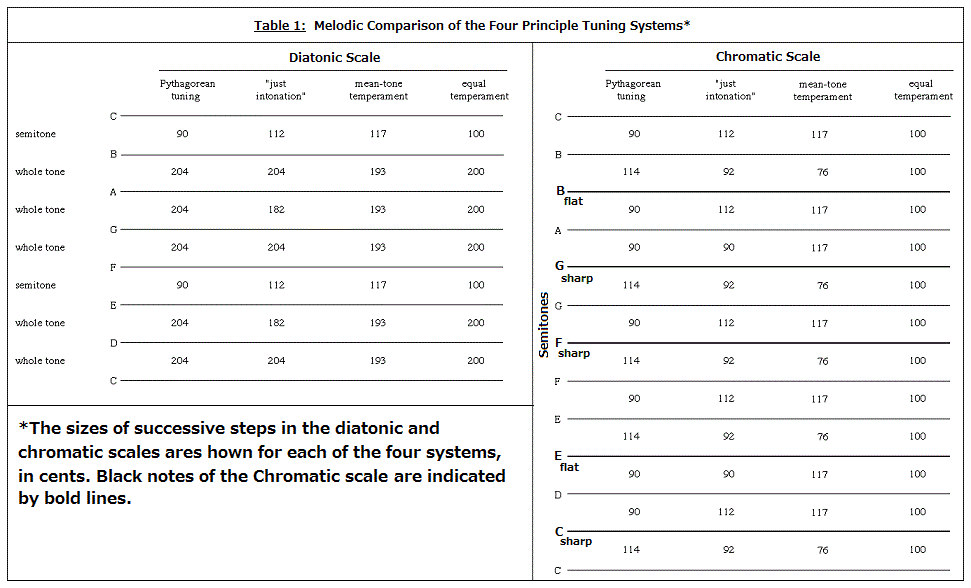

Ptolemaic tuning, often misleadingly named just intonation, sacrifices one of the fifths (D-A), which is altered to 40:27 from the simpler ratio 3:2, making it flat (too narrow) by a comma. The advantage of this system is that all the major thirds are true, or "in tune," as are all the major sixths except F-D, which is tuned to the ratio 27:16, as in the Pythagorean tuning (instead of to 5:3). The triad D-F-A is quite unusable, although the other triads used are perfectly in tune. (A triad is a chord built of two thirds.) For melody the system has the drawback of employing two different sizes of whole tones: C-D, F-G, and A-B are major tones (9:8, or 204 cents), and D-E and G-A are minor tones (10:9, or 182 cents). The difference is noticeable without being great enough to suggest that they are two purposely distinct intervals. To sing the first phrase of "Three Blind Mice" with the middle note perceptibly too high can hardly have seemed satisfactory at any period.

Although just intonation occupied the attention of many theorists, its disadvantages are so great that it is doubtful whether the system was ever strictly applied to harmonized music. Some kind of temperament may have been practiced empirically long before it was described in writing. The addition over several centuries of the five chromatic notes (the black notes of the piano), giving the full chromatic scale, certainly does nothing to improve either the Pythagorean or the Ptolemaic tuning (see Table 2, which shows the deviation of the four main tuning systems from the ideal tuning of the principal intervals). To either system the use of the chromatic notes adds more true fifths but also more untrue thirds and sixths. The advantages of just intonation over Pythagorean tuning are experienced only in chords made up of white notes. With the development of harmony and the increased use of chromatic notes, both tuning systems became increasingly unsatisfactory.

Temperament

The first mention of temperament is found in 1496 in the treatise Practica musica by the Italian theorist Franchino Gafori, who stated that organists flatten fifths by a small, indefinite amount. This practice tends to spread out the mistuning of the fifth D-A over several fifths, so that all are tolerable although none is perfect. This principle was systematized as mean-tone temperament, first described in 1523. Under this scheme, all the major thirds of the scale are made perfect (i.e., are tuned in the simple ratio 5:4); it results in an imperfection in the tuning of fifths that is spread out evenly over the entire cycle. Specifically, the interval of two octaves and a major third is tuned perfectly and divided into four fifths (C-G-d-a-e'), each of which has the ratio ⁴ʃ5:1 (compared to 3:2 for a perfectly tuned fifth). The fifths are flat by a quarter of a comma, which is much less dissonant than a comma: it gives a beat rate of 0.9 to 4 per second for fifths that fall within the compass of the medieval gamut. All major sixths are sharp by the same amount. Melodically, the scale resulting from mean-tone temperament is superior to the Ptolemaic (just intonation) scale, for all the whole tones are equal in size, being exactly half a true major third, or 193 cents. This is the source of the system's name: the mean, or average, whole tone. The semitones of the diatonic scale are relatively large, at 117 cents.

Mean-tone temperament, which was specifically designed for keyboard instruments, was an acceptable compromise so long as the black notes used in a composition did not extend beyond E♭ and G♯. As soon as D♯ was needed as well as E♭, the system collapsed. The keyboard provided only one key for E♭ and G♯. This key was tuned as E♭ and with no reference to the G♯ below it. The enharmonic fifth G♯-E♭ (in which E♭ is treated as equal to D♯) is nearly two commas out of tune in the mean-tone system. Worse even than the mistuned fifth of just intonation, it was often given the name "the wolf." Organs were occasionally built with split black keys so that E♭ and D♯ could be differently tuned and also A♭ and G♯. This expedient slightly extended the range of usable harmonies, but a more drastic remedy was soon needed. By spreading out the mistuning of the "wolf" fifth among its neighbours, in the same way that their predecessors had spread out the mistuning of the fifth D-A, musicians of the 17th century moved imperceptibly away from mean-tone temperament, in which the fifths are tuned unequally, toward the system of equal temperament, in which all fifths are equally flat.

In equal temperament, all intervals are made up of semitone units, each of which is set exactly at a 12th of an octave, or 100 cents. A fifth is built of seven semitones; in relation to a pure fifth, it is 2 cents flat. A major third is four semitones and is 14 cents sharp; a major sixth is nine semitones and is 16 cents sharp. Because in equal temperament the intervals are identical in all parts of the chromatic scale, the system is the only one that can accommodate the expanded range of harmonies of 19th- and 20th-century music. Melodically, it fulfills the ideal of equal steps. The price for these great advantages is the total disappearance of perfectly tuned intervals, save only the octave. For the piano and the harpsichord this is scarcely a drawback: the characteristic tone of these instruments is, in any case, rich in dissonant components. Indeed, it has been found that piano tuners systematically set octaves and even unison strings out of tune. But on the organ, with its purer and more sustained tone, the disadvantages of equal temperament are considered by many to outweigh its blessings. In England such musicians as the organist and composer Samuel Sebastian Wesley continued to oppose it even as late as the mid-19th century.

On fretted instruments—such as lutes, guitars, and viols—the frets extend across the fingerboard, producing at any one point divisions of equal lengths on strings of different pitch. Unless equal temperament is used, the positioning of the frets results in mistuned octaves and unisons when the same note is played on different strings. For this reason equal temperament was applied at least as early as the 16th century in the construction of fretted instruments.

It has often been stated that singers and players on instruments of undetermined tuning, such as violins and trombones, naturally use just intonation when performing together. Experimental evidence does not support this theory. In such circumstances musicians tend either to play in equal temperament, or, if anything, to distort intervals away from perfect consonance. Most probably this is the result of generations of conditioning. Moreover, it has been found that few musicians can distinguish melodically between just intonation and equal temperament and that those who can do so prefer the latter.

Tuning and musical history

It is seldom realized what an important effect tuning practices have had on the development of harmony and tonality. From the 10th to the 13th century thirds and sixths—now considered consonant—were treated as dissonances simply because, according to then-current tuning methods, they were dissonances. In Pythagorean tuning, only the bare fifth and octave could provide a tolerable point of repose in music accompanied by the organ. Although just intonation permitted some harmony based on triads, the use of sharpened leading notes (the last note of the scale, leading upward into the first), which by the 16th century had caused the older system of modes to disintegrate, was made acceptable only by the use of some kind of temperament. At a later date it was the existence of lutes tuned in equal temperament that made possible the more extreme experiments in chromaticism of composers such as Luca Marenzio and Don Carlo Gesualdo. The formation of a unified orchestra was probably delayed by the simultaneous practice of two incompatible tuning systems—mean-tone for keyboard instruments, equal temperament for lutes and viols. The decline of viols and their replacement by the violin family may have been hastened by the inability of viols to play with the organ. The modern orchestra began with the Vingt-quatre Violons du Roi (Twenty-four Violins of the King) of Louis XIV, and most later Baroque music is based on a keyboard instrument with from one to 30 members of the violin family playing in mean-tone temperament. The cycle of six related keys, established in the operas of Alessandro Scarlatti and the sonatas of Arcangelo Corelli and followed closely in most of the music of J.S. Bach and George Frideric Handel, is probably a direct outcome of mean-tone temperament. Within the limits of mean-tone temperament, the six keys exhaust the chromatic compass available. On the other hand, "wolf" chords may have been deliberately introduced by Domenico Scarlatti, François Couperin, and other composers to give an added piquancy to certain harpsichord passages. Many harpsichord players, including Bach, would retune a few notes of their instruments to prepare to play a piece in a new key, shifting the "wolf" fifth to part of the scale where it would do no harm. But in organ works such temporary retuning was hardly possible. Bach's organ tuning must have been as close to equal temperament as modern instruments are, although it is known that he was opposed to a strictly mathematical equality of intervals. By his title Well-Tempered Clavier he probably meant a kind of modified mean-tone temperament.

Enharmonic modulation, in which one note (say B♭) is treated as identical to another (say A♯) that actually has the same pitch only in equal temperament, was an exceptional device in Baroque music. But as orchestras became free of keyboard instruments and as keyboard instruments increasingly adopted equal temperament, it became a normal stock-in-trade, allowing the use of a series of key changes in one direction that eventually returns to the original key. Thus, it is not unusual for Mozart to complete the cycle of 12 keys in the course of a movement. Equal temperament permitted 19th-century composers to use the 12 notes of the chromatic scale with the utmost freedom. It also fixed those 12 notes so immutably in the Western musical consciousness that the revolutionary developments of 20th-century music, far from undermining them, have tended to perpetuate them.

Nicholas Temperley, Ed.: Professor of Musicology, University of Illinois at Urbana-Champaign. Author of The Music of the English Parish Church.

Works on tuning and temperament include Hermann von Helmholtz, Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik (1862; Eng. trans. by Alexander J. Ellis, On the Sensations of Tone, 1875), still the classic treatment of the subject, with useful additional observations by the translator;

J. Murray Barbour, Tuning and Temperament: A Historical Survey (1951), a comprehensive study of the theoretical aspects of the subject, with a good bibliography;

Llewelyn S. Lloyd and Hugh Boyle, Intervals, Scales and Temperaments (1963), designed for the musician; Paul C. Greene, "Violin Intonation," Journal of the Acoustical Society of America, 9:43–44 (1937), disposes of the theory that violinists naturally play in just intonation;

Roger E. Kirk, "Tuning Preferences for Piano Unison Groups," ibid., 31:1644–48 (1959), shows that musicians prefer groups of unison strings on the piano to be mistuned;

D.W. Martin and W.D. Ward, "Subjective Evaluation of Musical Scale Temperament in Pianos," ibid., 33:582–585 (1961), shows that musicians do not prefer just intonation to equal temperament;

Fritz A. Kuttner and J. Murray Barbour, The Theory of Classical Greek Music; Meantone Temperament in Theory and Practice; and The Theory and Practice of Just Intonation, Musurgia Records, Theory Series A, No. 1–3, an opportunity to hear the three major tuning systems that preceded equal temperament, both in scales and chords and in actual music.