page 60
Note: the contents of this page as well as those which precede and follow, must be read as a continuation and/or overlap in order that the continuity about a relationship to/with the dichotomous arrangement of the idea that one could possibly talk seriously about peace from a different perspective as well as the typical dichotomous assignment of Artificial Intelligence (such as the usage of zeros and ones used in computer programming) ... will not be lost (such as war being frequently used to describe an absence of peace and vice-versa). However, if your mind is prone to being distracted by timed or untimed commercialization (such as that seen in various types of American-based television, radio, news media and magazine publishing... not to mention the average classroom which carries over into the everyday workplace), you may be unable to sustain prolonged exposures to divergent ideas about a singular topic without becoming confused, unless the information is provided in a very simplistic manner.
Let's face it, humanity has a lousy definition, accompanying practice, and analysis of peace.
From acoustics there is a need to proceed to the notion of vibration when speaking of peace in terms of sociological dimensions of inquiry. Yet, in as much as some may want to constrain the definition of vibration to sounds related to political exigencies of consideration because this is the territorial limit of their main cognitive interest, it is of need to delve into those considerations of reverberation from other subject areas as well such as... to begin with, the field of molecular dynamics:
Molecular Vibrations When atoms join together in molecules, they can enter into characteristic vibrations and rotations. Just as an atom has a set of energy states associated primarily with the possible configurations of its electrons, so molecules have sets of energy states associated with their vibrations and rotations, as well as a set of electronic states. Light of the correct energy will induce changes from one vibrational (and/or rotational) state to another. Two ways in which isotopy relates to molecular vibrations, in particular, can be illustrated with the simplest of all molecules—diatomic molecules, which consist of only two atoms. Vibrational spectroscopy shows that isotopically heavier diatomic molecules have higher bond energies. (Bond energy is the amount of energy needed to separate the two atoms.) Quantum mechanical theory makes it possible to calculate from vibrational spectra just how much stronger the bond to the heavier isotope is. The differences between the chemical bond energies of isotopes help to explain why the isotopes do not behave identically in chemical reactions. The second relation concerns the spacing between vibrational energy levels: the vibrational energy levels of an isotopically heavier molecule lie closer together. Consequently, it takes less energy to excite 18O—18O from one vibrational level to the next than it does 16O—16O. Spectroscopists made good use of this fact when they inferred from the spectra of isotopically mixed diatoms the existence of previously unknown isotopes. Oxygen-18 was discovered in this way. Importance in the study of polyatomic molecules This second point, the distinguishability of the vibrational spectra of isotopically different molecules, is of great importance in the study of polyatomic molecules (molecules that contain three or more atoms). One key issue for chemists is the nature of the vibrations in polyatomic molecules: How do the nuclei of the atoms oscillate in relation to each other? The answer to this question bears strongly on what transient shapes the molecule may assume, how it will react with other molecules, and the rate at which it will do so. It is usually impossible to obtain this information from a study of the vibrational spectra of molecules made from atoms at natural abundance levels. Fortunately, the systematic substitution of heavier isotopes at known points in polyatomic molecules gives rise to new sets of vibrational spectra that clarify the nature of the atomic motions. There is a second, fundamental reason for investigating the vibrational spectra of isotopically substituted, or "labeled," molecules. In interpreting spectra, spectroscopists rely on the mathematical results of quantum theory. Often, a close analysis of vibrational spectra of labeled molecules offers the best means for testing the soundness of the prevailing theoretical understanding of molecules. Gregory F. Herzog: Professor of Chemistry, Rutgers University, New Brunswick, New Jersey.Source: "Isotope." Encyclopædia Britannica Ultimate Reference Suite, 2013. Phosphorescence Phosphorescence is related to fluorescence in terms of its general mechanism but involves a slower decay. It occurs when a molecule whose normal ground state is a singlet is excited to a higher singlet state, goes to a vibrationally excited triplet state via either an intersystem crossing or a molecular collision, and subsequently, following vibrational relaxation, decays back to the singlet ground state by means of a forbidden transition. The result is the occurrence of a long lifetime for the excited triplet state; several seconds up to several hours are not uncommon. These long lifetimes can be related to interactions between the intrinsic (spin) magnetic moments of the electrons and magnetic moments resulting from the orbital motion of the electrons. Molecules in singlet and triplet states react chemically in different manners. It is possible to affect chemical reactions by the transfer of electronic energy from one molecule to another in the reacting system. Thus the study of fluorescence and phosphorescence provides information related to chemical reactivity. |
Note: the reason for including the preceding and following comment about singlet and triple states is to correlate it with the presence of simple two-molecule bonding so that the reader would not get the impression that the "two" (pairing) is an isolated configuration without relational activity involving quantifiable patterns which do not exhibit the "two-pattern". In other words, "doublets" are not considered most commonly found, nor the most long lasting.
When a molecule changes its electronic state without direct absorption of light, as in nonradiative decay or internal conversion, it may go into a new excited state, which, left alone, would be short-lived (less than about 10-6 second); or it may go into a long-lived (metastable) excited state. Both types of reaction are known in photo-chemistry, but the long-lived states are particularly important in storing energy for chemical processes. The most important of the last named kind of transition is a Singlet >>> Triplet transition. Singlets and Triplets are electronic states that differ in having paired and unpaired electrons, respectively. Triplets are the most commonly found phosphorescing states. They cannot radiate rapidly and are therefore among the most long-lived excited species. For this reason triplets are frequently the primary products of photo-chemical reactions. Excited singlets are sometimes found, but they more often decay,...to triplets. Triplets can be identified by their magnetic properties; by contrast with singlets, the individual electron magnets of a triplet do not cancel each other so that triplets exhibit weak magnetism (paramagneticism), which can be detected by suitable techniques. |
Notice that "vibration" is not spoken of in terms of a single molecule and that they are grouped from the quantity of 3 and beyond with the word "polyatomic" just as primitive peoples used the word "many" in describing quantities greater than two. The notion of "soundness" can mean different things to different people because them may translate the word into coherence, sequential, logical, proportion, etc... It can also be used in describing a compilation of data to suggest that the compilation itself has some relevance to be considered. Take for example the following chart as illustrated on page 238 of the previously mention "Cognitive Basis of Science", in a chapter entitled "The Passionate Scientist: Emotion in Scientific Cognition" by Paul Thagard. It is a chart listing types of emotions deduced from an account given by James Watson about the discovery of the DNA structure:
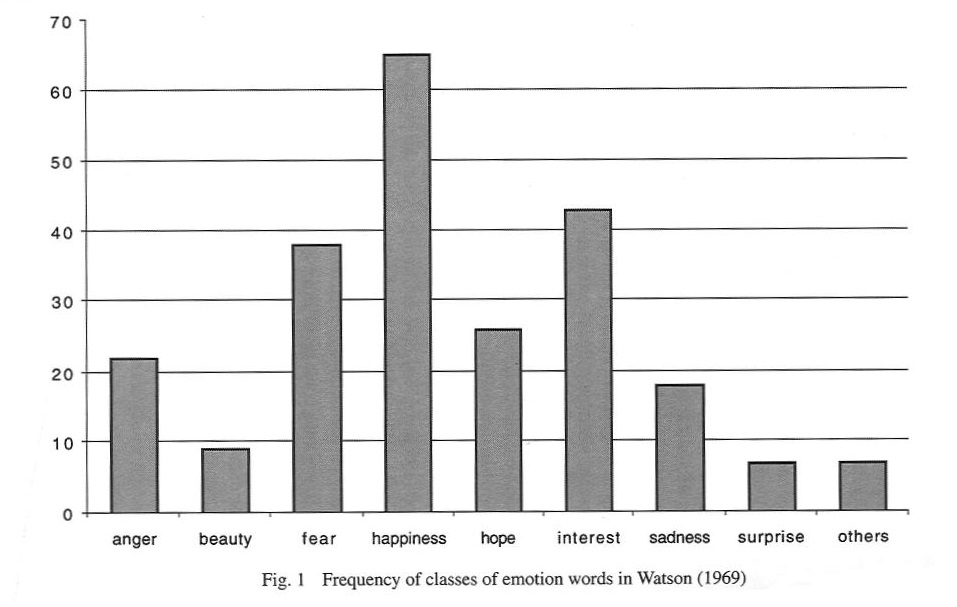
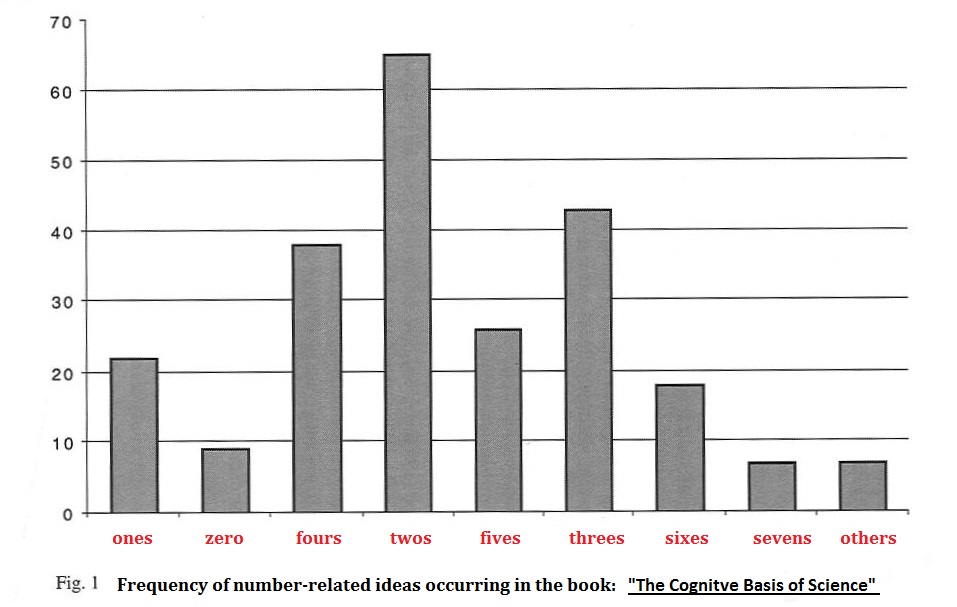
The types and amounts of different emotions are quantified, that is...associated with a numerical value... and yet the ideas throughout the book are not set into a similar frame of mind-reference with respect to quantification as a tell-tale sign of cognition related to those contributing ideas about cognition. In other words, the authors, as counters of scientific patterns, are not having their ideas subjected to the same type of quantitative analysis in order to describe how many times given numerical representations are being used in their descriptive analysis. It is the same over-sight occurring when peace is analyzed... as a representation of human cognition. But if we take the same chart and change the listing of items from emotions to numerical indices related to the numerical patterns of ideas, we arrive at a hypothetical representation concerning the contents of the book from which the above chart was garnered. The chart is not meant to relate to the actual occurrences of number-patterned ideas distributed in the book, but as a simplified illustration of an alternative approach at understanding human cognition we can apply to the analysis of peace.
However, in the present context related to this page's selection involving the presentation of vibration in terms of molecular states, is meant as a metaphor to the present discussion and not meant as a direct symbolic substitute of actual activity beyond the presence of a suppositional translation between different subject matter. In other words, though correlations can be made and terms shared to represent generalities, this should not dispose the reader to consider that a direct one -to- one correspondence is indicated or be taken in any literal sense without an attendant inter-relational attribution presented to make such a case.
For example, while many people have viewed human society in terms of their observations of an ant or bee colony, and that the Queen, Drone, Worker divisions correspond to upper, middle, and lower classes, it is we humans who have imposed the correlation and not the other way around... unless one wants to think in terms of a science fiction scenario in which humans are a macroscopic version of microscopic events occurring in life. We customarily engage in devising group distinctions which can be enumerated, and that the enumerations can thus be subjected to an analysis, but this third extension rarely takes place. Primary and secondary analysis occur, and these may be compounded with their own primary and secondary excursions, but there is no tertiary formulation adopted. Though we recognize patterns that may be further subjected to a pattern of quantification, an overall tabulation of quantification as an expression of cognition is not itself subjected to a tabled analysis. Most often, yet another area of consideration is subjected to primary and secondary forms of analysis, but these do not then acquire an additional level of analysis. Such is the case in the analysis of peace. It has customarily been subjected to a primary and secondary ordering of contemplation, but instead of proceeding to a tertiary detection, segments of the primary and secondary perspectives are thus subjected to their own primary and secondary models of analysis which gives the impression of a greater detailed analysis of the primary subject, but is instead a detailed analysis of primary and secondary details. It is like counting out one and two jelly beans and then dissecting the two jelly beans into their own compartmentalizations of analysis, but no third jelly bean is ever counted because the time, effort and expenditure put into the two is used to define a presumption that any more than two would simply be a repetition of what has already occurred. In other words, the "three" is termed "many" or "much of the same".
While some people may think that an analysis of peace has been exhausted because there is an over-riding assumption that there will never be peace, such an assumption is based upon an assumption derived from the cognitive profile of those whose brains do not think beyond the quantity of "two" such as describing peace as being a representative state of existence without war. In other words, they have difficulty seeing past this dichotomy because their brains are chained to a two-patterned orientation... even if they use multiple examples as a means of suggesting to themselves they think beyond the basic cognitive pattern of two. And though one can provide multiple types of alternative ways in looking at an analysis of peace, all of them are subjected to personal forms of reductionism so as to construct yet another pattern-of-two for those whose mentality recurringly subject their perceptions to this formula. Nonetheless, for those whose minds actually are more receptive to alternative perceptions of analytical inquiry, let us look at another "vibration" representation in terms of physical sensation such as touch, as opposed to a strict auditory form, and follow it with additional references such as pointing out how vibration is linked to repetition which results in unfavorable medical conditions, and must be considered as much a problem of vibration as can the repetition of analysis which lead humanity no where:
Vibration reception Adaptation and recovery occur most rapidly among touch receptors, and they tend to respond well to repeated stimulation, even of relatively high frequency. Thus, a person can feel whether an object is vibrating; above a threshold frequency of about 15 cycles per second (cps), discretely perceived tactual stimuli seem to fuse into a quite new and distinct vibratory sensation. The upper frequency limit of this vibration sense is found at several thousand cps among normal individuals, with sensitivity being maximal in the range of 200 cps (above a threshold amplitude of about 100 millimicrons). Just as pitch is discriminated in hearing, differences of about 12 to 15 percent in vibration frequencies can be distinguished by most people. Vibration sensitivity is not limited to man; fish, for instance, also may respond to low-frequency water vibrations with tactile receptors. In addition, several kinds of animals have special vibration receptors. In some insects, a group of specialized structures (chordotonal sensilla) in the upper part of each tibial segment of the leg signal vibrations from the ground below. In the cockroach, the threshold amplitude for vibrational stimuli of this kind has been found to be less than 0.1 millimicron. Birds have special receptors (corpuscles of Herbst in the tibiotarsal bone of the leg) with which they can detect slight vibrations of the twig or branch on which they sit. Perhaps birds are alerted at night in this way to approaching predators; maximal sensitivity is at about 800 cps, and the threshold amplitude is close to 20 millimicrons. Spiders also use their vibration sense to locate prey in the web. Sven Dijkgraaf: Emeritus Professor of Comparative Physiology, State University of Utrecht, The Netherlands.Source: "Mechanoreception." Encyclopædia Britannica Ultimate Reference Suite, 2013. Vibration (Occupational disease) Whole-body vibration is experienced in surface and air transport, with motion sickness its most familiar effect. A more serious disorder, known as Raynaud's syndrome or vibration white finger (VWF), can result from the extensive use of vibratory hand tools, especially in cold weather. The condition is seen most frequently among workers who handle chain saws, grinders, pneumatic drills, hammers, and chisels. Forestry workers in cold climates are particularly at risk. Initial signs of VWF are tingling and numbness of the fingers, followed by intermittent blanching; redness and pain occur in the recovery stage. In a minority of cases the tissues, bones, and joints affected by the vibration may develop abnormalities; even gangrene may develop. VWF can be prevented by using properly designed tools, avoiding prolonged use of vibrating tools, and keeping the hands warm in cold weather. Other mechanical stresses Muscle cramps often afflict workers engaged in heavy manual labour as well as typists, pianists, and others who frequently use rapid, repetitive movements of the hand or forearm. Tenosynovitis, a condition in which the sheath enclosing a tendon to the wrist or to one of the fingers becomes inflamed, causing pain and temporary disability, can also result from prolonged repetitive movement. When the movement involves the rotation of the forearm, the extensor tendon attached to the point of the elbow becomes inflamed, a condition commonly known as tennis elbow. George Kazantzis: Visiting Professor, Imperial College of Science, Technology, and Medicine, University of London; former Professor of Occupational Medicine, London School of Hygiene and Tropical Medicine. Contributor to Handbook on the Toxicology of Metals.Source: "Occupational disease." Encyclopædia Britannica. From Britannica article on String Theory: Predictions and theoretical difficulties String theory was an intuitively attractive proposal, but by the mid-1970s more-refined measurements of the strong force had deviated from its predictions, leading most researchers to conclude that string theory had no relevance to the physical universe, no matter how elegant the mathematical theory. Nevertheless, a small number of physicists continued to pursue string theory. In 1974 John Schwarz of the California Institute of Technology and Joel Scherk of the École Normale Supérieure and, independently, Tamiaki Yoneya of Hokkaido University came to a radical conclusion. They suggested that one of the supposedly failed predictions of string theory—the existence of a particular massless particle that no experiment studying the strong force had ever encountered—was actually evidence of the very unification Einstein had anticipated. Although no one had succeeded in merging general relativity and quantum mechanics, preliminary work had established that such a union would require precisely the massless particle predicted by string theory. A few physicists argued that string theory, by having this particle built into its fundamental structure, had united the laws of the large (general relativity) and the laws of the small (quantum mechanics). Rather than merely being a description of the strong force, these physicists contended, string theory required reinterpretation as a critical step toward Einstein's unified theory. The announcement was universally ignored. String theory had already failed in its first incarnation as a description of the strong force, and many felt it was unlikely that it would now prevail as the solution to an even more difficult problem. This view was bolstered by string theory's suffering from its own theoretical problems. For one, some of its equations showed signs of being inconsistent; for another, the mathematics of the theory demanded the universe have not just the three spatial dimensions of common experience but six others (for a total of nine spatial dimensions, or a total of ten space-time dimensions). Dimensions and vibrations Because of these obstacles, the number of physicists working on the theory had dropped to two— Schwarz and Michael Green, of Queen Mary College, London—by the mid-1980s. But in 1984 these two die-hard string theorists achieved a major breakthrough. Through a remarkable calculation, they proved that the equations of string theory were consistent after all. By the time word of this result had spread throughout the physics community, hundreds of researchers had dropped what they were working on and turned their full attention to string theory. Within a few months, string theory's unified framework took shape. Much as different vibrational patterns of a violin string play different musical notes, the different vibrations of the tiny strands in string theory were imagined to yield different particles of nature. According to the theory, the strings are so small that they appear to be points—as particles had long been thought to be—but in reality they have length (about 10-33 cm); the mass and charge of a particle is determined by how a string vibrates. For example, string theory posits that an electron is a string undergoing one particular vibrational pattern; a quark is imagined as a string undergoing a different vibrational pattern. Crucially, among the vibrational patterns, physicists argued, would also be the particles found by experiment to communicate nature's forces. Thus, string theory was proposed as the sought-for unification of all forces and all matter. What of the six extra spatial dimensions required by string theory? Following a suggestion made in the 1920s by Theodor Kaluza of Germany and Oskar Klein of Sweden, string theorists envisioned that dimensions come in two distinct varieties. Like the unfurled length of a long garden hose, dimensions can be big and easy to see. But like the shorter, circular girth of the garden hose, dimensions can also be far smaller and more difficult to detect. This becomes more apparent by imagining that the circular cross section of the garden hose is shrunk ever smaller, below what can be seen with the naked eye, thereby misleading a casual observer into thinking the garden hose has only one dimension, its length. Similarly, according to string theory, the three dimensions of common experience are large and hence manifest, while the other six dimensions are crumpled so small that they have so far evaded detection. During the decade from 1984 to 1994, many theoretical physicists strove to fulfill string theory's promise by developing this abstract, wholly mathematical framework into a concrete, predictive theory of nature. Because the infinitesimal size of strings has precluded their direct detection, theorists have sought to extract indirect implications of the theory that might be testable. In this regard, the extra dimensions of string theory have proved a major hurdle. Imagining these extra dimensions as small and hidden is a reasonable explanation for their apparent absence. However, also because strings are so small, they would vibrate in every dimension, not just in the usual three dimensions. Studies showed that, much as the shape and size of a French horn affect the vibrational patterns of air-streams coursing through the instrument, the exact shape and size of the extra dimensions would affect how strings vibrate. And since the strings' vibrations determine quantities such as particle masses and charges, predictivity requires knowledge of the geometrical form of the extra dimensions. Unfortunately, the equations of string theory allow the extra dimensions to take many different geometric forms, making it difficult to extract definitive testable predictions. Brian R. Greene: Professor of Physics and of Mathematics, Columbia University. Author of The Elegant Universe and others.Source: "String Theory." Encyclopædia Britannica. Transduction of mechanical vibrations (From "Human Ear" article) The hair cells located in the organ of Corti transduce mechanical sound vibrations into nerve impulses. They are stimulated when the basilar membrane, on which the organ of Corti rests, vibrates. The hair cells are held in place by the reticular lamina, a rigid structure supported by the pillar cells, or rods of Corti, which are attached to the basilar fibres. At the base of the hair cells is a network of cochlear nerve endings, which lead to the spiral ganglion of Corti in the modiolus of the cochlea. The spiral ganglion sends axons into the cochlear nerve. At the top of the hair cell is a hair bundle containing stereocilia, or sensory hairs, that project upward into the tectorial membrane, which lies above the stereocilia in the cochlear duct. (The single kinocilium, which is found on the hair cells of the vestibular system, is not found on the receptor cells of the cochlea.) When the basilar membrane moves upward, the reticular lamina moves upward and inward; when the membrane moves downward, the reticular lamina moves downward and outward. The resultant shearing forces between the reticular lamina and the tectorial membrane displace or bend the longest of the stereocilia, exciting the nerve fibres at the base of the hair cells. The mechanism the hair cell uses to convert sound into an electrical stimulus is not completely understood, but certain key features are known. One of the most important aspects of this process is the endocochlear potential, which exists between the endolymph and perilymph. This direct current potential difference is about +80 millivolts and results from the difference in potassium content between the two fluids. It is thought to be maintained by the continual transport of potassium ions from the perilymph into the cochlear duct by the stria vascularis. The endolymph, which has a high potassium level and a positive potential, is contained in the cochlear duct and thus bathes the tops of the hair cells. The perilymph, which has a low potassium level and a negative potential, is contained in the scala vestibuli and scala tympani and bathes the lower parts of the hair cells. The inside of the hair cell has a negative intracellular potential of -60 millivolts with respect to the perilymph and -140 millivolts with respect to the endolymph. This rather steep gradient, especially at the tip of the cell, is thought to sensitize the cell to the slightest sound. The stereocilia are graded in height, becoming longer on the side away from the modiolus. All the stereocilia are interlinked so that, when the taller ones are moved against the tectorial membrane, the shorter ones move as well. The mechanical movement of this hair bundle generates an alternating hair cell receptor potential. This occurs in the following manner. When the stereocilia are bent in the direction of increasing stereocilia length, ion channels in the membrane open, allowing potassium ions to move into the cell. The influx of potassium ions excites, or depolarizes, the hair cell. However, when the stereocilia are deflected in the opposite direction, the ion channels are shut and the hair cell is inhibited, or hyperpolarized. The depolarization of the cell stimulates the release of chemicals called neuro-transmitters from the base of the hair cell. The neuro-transmitters are absorbed by the nerve fibres located at the basal end of the hair cell, stimulating them to send an electrical signal along the cochlear nerve. The outer hair cells contain both actin and myosin, the same contractile proteins that make up muscles, and this allows the cells to contract rhythmically in response to tonal stimuli. Recent studies suggest that the cells themselves may be tuned structures. The ability of an outer hair cell to respond to a particular frequency may depend not only on its position along the length of the basilar membrane but also on its mechanical resonance, which probably varies with the length of its bundle of stereocilia and with that of its cell body. The inner hair cells are much more uniform in size. Local groups of outer hair cells act not only as detectors of low-level sound stimuli, but, because they can act as mechanical-electrical stimulators and feedback elements, they are believed to modify and enhance the discriminatory responses of the inner hair cells. How they do this is not understood. Because the inner hair cells rest on the bony shelf of the osseous spiral lamina rather than on the basilar membrane, they are presumably less readily stimulated by the traveling wave. Help from the outer hair cells may be required to generate the signal that the inner cells transmit synaptically to the fibres of the cochlear nerve. Experiments in animals have shown that, when the outer hair cells of the basal turn have been destroyed by the ototoxic action of the antibiotic kanamycin, the inner hair cells in the same region can still respond to sound, but their thresholds are elevated by about 40 decibels. Remarkably, the cochlea itself actually produces sounds. Its otacoustic emissions can be spontaneous or evoked by external acoustic stimulation. These emissions are thought to be produced by rhythmical contractions of the cochlear hair cells. Although faint, they can be recorded with a small microphone placed in the external canal; they are absent when there has been extensive loss of hair cells from the basal turn, as in cases of presbycusis or ototoxicity. While these emissions challenge some earlier concepts of the micro-mechanisms of cochlear function, they are proving increasingly useful in the audiological evaluation of impaired hearing, in adults as well as infants. Joseph E. Hawkins: Emeritus Professor of Otolaryngology (Physiological Acoustics), Medical School, University of Michigan, Ann Arbor. Editor of Otophysiology.Source: "Ear, Human." Encyclopædia Britannica. |
Whereas we do not customarily view peace (or war) in terms of (sociological or environmental) vibrations, we can do so from either a cause or an effect proposition. (Peace and war can either be viewed as causing social vibrations or be the vibrating result of one or more particular events.) It is particularly peculiar that we can adopt the concept of three spatial dimensions but not include the notion of three types/forms (formulas) of string theory. No less, we could also include the notions of theoretical physics positions which are illustrated by other types of vibrating surfaces or mechanisms such as the surface of a drum, valve placement, reed, or what have you. In other words, instead of vibrating strings would could speak in terms of vibrating reeds of metal, or vibrating tonsils or vibrating tongue, etc..., of which it is value to include a reference to vibrations related to the mechanism of hearing. However, supplying different analogies in an analysis of peace does not necessarily provide the impetus for seeking to create a sustained peace if those reading this series of essays are bent towards identifying means by which peace can be averted since they can acquire more of what they want by an application of war in one form or another.
Reference to the human ear was made on page 2 in this series.
Date of Origination: Thursday, 20-April-2017... 03:12 AM
Date of initial posting: Sunday, 11-June-2017... 8:31 AM
Updated posting: Saturday, 31-March-2018... 1:03 PM