page 56
Note: the contents of this page as well as those which precede and follow, must be read as a continuation and/or overlap in order that the continuity about a relationship to/with the dichotomous arrangement of the idea that one could possibly talk seriously about peace from a different perspective as well as the typical dichotomous assignment of Artificial Intelligence (such as the usage of zeros and ones used in computer programming) ... will not be lost (such as war being frequently used to describe an absence of peace and vice-versa). However, if your mind is prone to being distracted by timed or untimed commercialization (such as that seen in various types of American-based television, radio, news media and magazine publishing... not to mention the average classroom which carries over into the everyday workplace), you may be unable to sustain prolonged exposures to divergent ideas about a singular topic without becoming confused, unless the information is provided in a very simplistic manner.
Let's face it, humanity has a lousy definition, accompanying practice, and analysis of peace.
In our attempted enhanced analysis of peace (and thus war and inter-mediation as well), it may seem to some that we are pursuing the development of a "peace-science"... or in other words, a science of peace... any by such an attribution we are somehow automatically delving into something that will be lucratively beneficial— at least from a "cognitive science" perspective. Yet, it must be understood that those engaged in pursuing an appreciation of the "cognitive" basis (origin, process, application) of science are using an approach of reverse engineering. They present us with what are assumed to be examples of "scientific thinking" because particular ideas are thus labeled a science-approach, and then construe to reveal what they may describe as a generality of mental accommodation being used by all scientists, though individual scientists may develop their ideas by emphasizing one aspect or elemental characteristic over another that yet another scientist might be inclined to use an emphasized alternative tool of cognition... or thinking.
For example, a cognitive "scientist" or "lay" person (as the distinction is usually laid out in a dichotomous fashion)... may compile a running list (on paper or in memory) of various "scientific efforts" or efforts of those whose activities have become to be labeled as being scientific endeavors; and create what they believe to be (paired) similarities— though their usage of a two-patterned approach may well be overlooked. However, those engaged in reading the efforts of such cognitive "scientists" may then make a comparison of them in yet another two-patterned approach. Amongst most or all of them we may not find a single one who proceeds from such a two-patterned effort of comparison into the usage of a tripartite configuration, even though all of them may represent their ideas of (two-patterned) comparison with a three-patterned model displaying numbers (such as 1, 2, 3), letters (such as A, B, C or X, Y, Z), or some geometric model involving a linear-circular-triangular configuration, though alternatives may be employed such as circle-square-triangle, etc... While they are engaged in an attempted analysis of others ideas using an unrecognized (two-patterned) comparative model (that may be stated in a three-patterned way), they remain oblivious that all the human minds are utilizing a basic one, two, three formula characteristically identified in developmental biology set within a closed environmental system that is incrementally decaying.
In one or another fashion that may be personalized, so-called "cognitive scientists" or "cognitive psychologists" are trying to reverse engineer the mechanics of (scientific, everyday/folk, "creative/original/genius" or otherwise non-normal thinking [neurotic, socio-pathic, psychotic, etc...]). In some instances the attempt is to construct a model of what is being described as "scientific thinking" which will enable to apply (predict and control) a generic illustration that can be understood by most, if not all people, when given the appropriate legend for understanding their particular map of the human thinking processes. Some of these researchers or at least those interested in their research, have an interest in acquiring a means by which they can make themselves think "scientifically" (considered to be a better way of thinking by some standards of interpretation); and thus apply such thinking to their interest, whatever it may be... so that they can discover some great truth, construct an idea that will improve their economic circumstances, or be able to impose their views on others in order to manipulate them to do their bidding. Others of course seek to apply such a generic model as a generously given teaching tool to improve education standards. It is their hope that by creating a greater understanding of how scientific thinking works... because it is assumed that their exists an underlying universality that can be used as a skeleton key by anyone in any subject area... so long as they follow some purported manual for thinking scientifically... which could well involve a given dietary, social, and personal experience regime... contoured by established rules-of-development for creating scientific paradigms of thought in childhood.
Indeed, with such a proposed manual one might consider the possibility of being able to enhance the thinking of humanity's entire Earthly population... except that it must be noted there are those who can think scientifically but are morally evil. The idea of an "evil genius" may come to mind for some readers and cause them to be afraid of the development of such a manual being used by those with criminal intentions... or by those in legislative, executive or judicial bodies whose primary interest is their own career... no matter who gets hurt or what gets destroyed. Such a reversed engineered manual or "cookbook" of recipes that could be used by others to bake up a concoction that is a single (self-) serving or serves a few (such as in a corporation or department within a government or individual in an association), does not mean it will be used for good reasons. The fact that even cognitive scientists don't selflessly work together for the betterment of humanity instead of their own personal career interests is a testament to the existence of personal self-interests. They don't mind sharing their ideas so long as they are duly recognized for such ideas and that they alone are enabled to control how, when, where, and by whom such ideas can be used. In other words, the idea of working in total obscurity like some artist or poet living in privation... and then dying without every gaining recognition is the exception and not the rule. Such a situation must be acknowledged in any "cognitive manual" to be generically offered to the public... whose sales are then used to enrich the lives of the creator(s) of such a manual. Hence, there is a commercialization to be recognized as part of the "scientific process". It is quite rare to find someone who works solely for enhanced understanding without expecting some measure of recognition... at the very least amongst those who share a similar vein of thought.
With respect to cognition displaying a progression from one, to two, to three... it is of need to realize such a transition may not take place completely, coherently or without leaps. In other words, one may acknowledge the presence of a prominent two and three, the "one" may not be so salient a characteristic. However, the "one and two" might well be compartmentalized into a pairing such as "major premise-minor premise", with the third position noted as an add-on feature such as "conclusion". There can also be individual representations which encompass three (or more) individualities such as in the case of the keyboard as described on page 53 of this 'peace' series which describes a three-in-one (ratio) reference:
Only in Europe did the keyboard develop—for reasons that are not clear. The principle of the keyboard has been used successfully to control:
- Bells (the carillon)
- Plucked and struck stringed instruments (the piano and harpsichord)
- Wind instruments (the organ, the accordion, and the harmonium).
The reason for such is clear if we taken into consideration that we can view Europeans as the "3rd born" race (Africans... Asians... Caucasians) within the structural placement of the old crudely described racial lineage of development. (Africans appeared first on the scene of humanity, Asians became the next dominant arrival, followed by Caucasians). If we then couple this to the embraced orientations of dominant thinking such as the Chinese adopting a two-patterned interpretation of reality identified in the yin/yang concept, and Europeans moving towards the usage of various three-patterned ideas (3 laws of motion, 3 laws of planetary motion, Roman usage of first-middle-last names to signify a person, Trinitarianism, [Dumezilian] tripartite ideology, [3-part] syllogisms, Trigonometry, etc.. In such cases, singularity can be defined by enhanced practices of tribalism and thus easier to understand for the many African cultures in antiquity... though Asian and Caucasians have likewise experienced some occasions of this "selfie" singularity). Hence, human cognition developing along a one, two, three sequence... or at least some variation thereof, can be seen in the evolutionary development of civilizations, if not earlier bi-pedal human-like creatures as well, which served as precursors to overall human sentience... whether or not a direct-line descendance can be identified; and thus suggests an environmentally-based imposition for the development of such an exercised cognitive pattern showing up within the means attributively possible for a given type of hominine.
With respect to the developmental usage of trigonometry which can be described as a "European-oriented" cognitive formulation, its presence in ancient Egypt (that some may argue to be at the transitional juncture between Africa and Europe— by way of the Middle East), is an item of cognition that we of today may see in "whole" terms when set against the usage of Pyramid construction (in that we typically visualize all four sides), but ancient Egyptians conceptualized as four independent structures. The reason for saying this is illustrated in the way they portrayed human figures. There is a clear lack of illustrated depth because the figures are show with both shoulders "laid flat" on the surface of stone. It is as if the illustrated figures in a scene were faced in one direction while their body was faced toward another. While the inability to capture depth in painting does not necessarily have to equate with an inability to see depth, it is necessary to remember how similar architectural renderings are to artistic portrayals. With respect to trigonometry, the view that a side of a pyramid was seen as an isolated (independent) structure seen from different geographical perspectives (north-south-east-west), though there are only two (cognitively) recognized seasons of cultivation in Egypt (summer-winter)... which no doubt had some influence on thinking orientations; can be seen in the following reference to the origination of trigonometry and its usage.
However, the application of trigonometry relied on the vertical and horizontal (rise and run... having some reference to the solar event), with the diagonal (slope) as an "add on" third component similar to the case of the "conclusion" seen in the syllogistic form of "Major Premise-Minor Premise—conclusion", with the usage of beginning letter capitals in the former and small beginning letter for the latter, a means of illustrating the prominence of the first two and the third as a type of tag-along. (In other words, the "Major/Minor" aspect is the emphasis of a dominant dichotomy preceding the fledgling presence of a third component as a beginning arrival of a third type of cognitive component.) This latter point is illustrated when the "rise and run" aspects described as vertical and horizontal play a prominent part in describing the after-math occurrence of a third component such as in the science of artillery-based warfare concerning parabolic trajectories. In other words, if two elements are known, the third element is necessarily a logical given, and is of little value without the first two. In such conceptualizations, the third component is a "natural" outcome (like the birth of a child) which can not be generated with two important originating parts (man and woman).
Separating the two, like separating a man and woman, is tantamount to ensuring the third component would never be born in order to be conceptualized and later develop into its own separate self... even though human cognition has not evolved such a character in any real sense. The "tripartite" third component of human cognition remains tethered to past compilations of dichotomies instead of making its own way in the form of a new type of separate cognition which represents an actual third and separate identity realm akin to a new evolutionary stage of brain development. In many instances the idea of an historical development of human cognition in terms of a one-two-three pattern does not come to mind and therefore the idea of developmental (fledgling) or transitional stage representations (which may waver to and fro), may not come to the mind of a reader. In some instances one or two people may "dabble" in a progressive mental realm only to become embroiled in a former (pre-stage of) development because such an orientation is the dominant orientation of the smartest people in a given culture in which the person is forced to find some semblance of a relative measure of living... and thus thinking like everyone else. For example, a "prelude" to trigonometry is not itself a representative cognitive condition of trigonometry. Likewise, providing Nobel Prizes to those whose actions or words are interpreted to be representative of or related to "peace", is not the same as a measurable value which will lead us to a sustained peace. Hence, there must be an awareness of "experimental models" that are dead ends, like so many trial and error activities have been in different subject areas.
It is of interest to point out that in terms of a line-circle-triangle... developmental progression of human cognition of which there are multiple examples as seen on page 29 in this 'peace' series, the "3rd" cognitive component is cast within the second "circular" cognitive component... that is if we can view the square as a line + line + line + line "linear" configuration and the circle as singular object, with the triangle as a difficult to interpret line-object with unequal lines compiled to form a singular object. If such a cognitive progression is real, and not some imaginative intellectualism, then the placement of a triangle within a circle (or square) defines the circle and square as being dominant architectures of thought with the triangle as that "born within", and not the other way around such as "squaring the circle", "circling the square", "squaring the triangle", "triangulating the square", or "triangulating the circle", "squaring the square", "circling the circle", as well as "triangulating the triangle"... by means other than the obvious. The usage of pairing in terms of proportionality is overlooked with the proportionality involves more than two elements... yet, the cognitive activity of "two" is nonetheless used. Proportionality is not moving beyond the "two" attribute of cognitive activity as is seen when peace and war are viewed as a "proportioned" contrast. It's similar to the usage of the language employed in physics-related scientific analysis where one speaks of "half-lifes" with respect to decay as a measuring tool. Thus, the "half-life" reference is little more than a substitute for "two-patterned" thinking. (If you take one and halved, it, you end up with "two" that can become misunderstood as a separate "two" identity without any increase in intellectual development having actually occurred in an evolutionary-developmental sense. While the "two" from a one-source would seem to suggest a cognitive advancement, it is merely a transitional phase... a precursor alluding to an advancement.)
History of trigonometry Classical trigonometry Ancient Egypt and the Mediterranean world Several ancient civilizations—in particular, the Egyptian, Babylonian, Hindu, and Chinese—possessed a considerable knowledge of practical geometry, including some concepts that were a prelude to trigonometry. The Rhind papyrus, an Egyptian collection of 84 problems in arithmetic, algebra, and geometry dating from about 1800 BC, contains five problems dealing with the seked. A close analysis of the text, with its accompanying figures, reveals that this word means the slope of an incline—essential knowledge for huge construction projects such as the pyramids. For example, problem 56 asks: "If a pyramid is 250 cubits high and the side of its base is 360 cubits long, what is its seked?" The solution is given as 51/25 palms per cubit; and since one cubit equals 7 palms, this fraction is equivalent to the pure ratio 18/25. This is actually the "run-to-rise" ratio of the pyramid in question—in effect, the cotangent of the angle between the base and face (see the figure). It shows that the Egyptians had at least some knowledge of the numerical relations in a triangle, a kind of "proto-trigonometry." 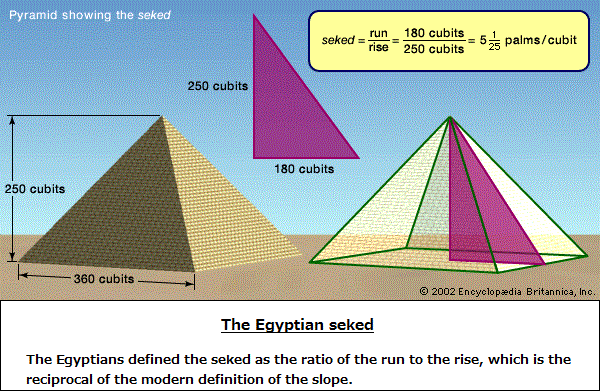 The word trigonometry comes from the Greek words trigonon ("triangle") and metron ("to measure"). Until about the 16th century, trigonometry was chiefly concerned with computing the numerical values of the missing parts of a triangle (or any shape that can be dissected into triangles) when the values of other parts were given. For example, if the lengths of two sides of a triangle and the measure of the enclosed angle are known, the third side and the two remaining angles can be calculated. Such calculations distinguish trigonometry from geometry, which mainly investigates qualitative relations. Of course, this distinction is not always absolute: the Pythagorean theorem, for example, is a statement about the lengths of the three sides in a right triangle and is thus quantitative in nature. Still, in its original form, trigonometry was by and large an offspring of geometry; it was not until the 16th century that the two became separate branches of mathematics. Ancient Egypt and the Mediterranean world 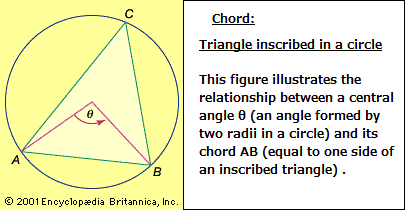
Trigonometry in the modern sense began with the Greeks. Hipparchus (c. 190-120 BC) was the first to construct a table of values for a trigonometric function. He considered every triangle—planar or spherical—as being inscribed in a circle, so that each side becomes a chord (that is, a straight line that connects two points on a curve or surface, as shown by the inscribed triangle ABC in the figure). To compute the various parts of the triangle, one has to find the length of each chord as a function of the central angle that subtends it—or, equivalently, the length of a chord as a function of the corresponding arc width. This became the chief task of trigonometry for the next several centuries. As an astronomer, Hipparchus was mainly interested in spherical triangles, such as the imaginary triangle formed by three stars on the celestial sphere, but he was also familiar with the basic formulas of plane trigonometry. In Hipparchus's time these formulas were expressed in purely geometric terms as relations between the various chords and the angles (or arcs) that subtend them; the modern symbols for the trigonometric functions were not introduced until the 17th century. (See the following table of common trigonometry formulas.)  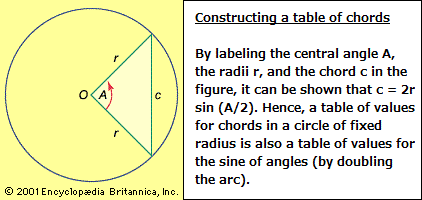
The first major ancient work on trigonometry to reach Europe intact after the Dark Ages was the Almagest by Ptolemy (c. AD 100-170). He lived in Alexandria, the intellectual centre of the Hellenistic world, but little else is known about him. Although Ptolemy wrote works on mathematics, geography, and optics, he is chiefly known for the Almagest, a 13-book compendium on astronomy that became the basis for mankind's world picture until the heliocentric system of Nicolaus Copernicus began to supplant Ptolemy's geocentric system in the mid-16th century. In order to develop this world picture—the essence of which was a stationary Earth around which the Sun, Moon, and the five known planets move in circular orbits—Ptolemy had to use some elementary trigonometry. Chapters 10 and 11 of the first book of the Almagest deal with the construction of a table of chords, in which the length of a chord in a circle is given as a function of the central angle that subtends it, for angles ranging from 0° to 180° at intervals of one-half degree. This is essentially a table of sines, which can be seen by denoting the radius r, the arc A, and the length of the subtended chord c (see the figure), to obtain c = 2r sin A/2. Because Ptolemy used the Babylonian sexagesimal numerals and numeral systems (base 60), he did his computations with a standard circle of radius r = 60 units, so that c = 120 sin A/2. Thus, apart from the proportionality factor 120, his was a table of values of sin A/2 and therefore (by doubling the arc) of sin A. With the help of his table Ptolemy improved on existing geodetic measures of the world and refined Hipparchus' model of the motions of the heavenly bodies. India and the Islamic world The next major contribution to trigonometry came from India. In the sexagesimal system, multiplication or division by 120 (twice 60) is analogous to multiplication or division by 20 (twice 10) in the decimal system. Thus, rewriting Ptolemy's formula as c/120 = sin B, where B = A/2, the relation expresses the half-chord as a function of the arc B that subtends it—precisely the modern sine function. The first table of sines is found in the Ā-ryabhat.i-ya. Its author, Ā-ryabhat.a I (c. 475-550), used the word ardha-jya for half-chord, which he sometimes turned around to jya-ardha ("chord-half"); in due time he shortened it to jya or jiva. Later, when Muslim scholars translated this work into Arabic, they retained the word jiva without translating its meaning. In Semitic languages words consist mostly of consonants, the pronunciation of the missing vowels being understood by common usage. Thus jiva could also be pronounced as jiba or jaib, and this last word in Arabic means "fold" or "bay." When the Arab translation was later translated into Latin, jaib became sinus, the Latin word for bay. The word sinus first appeared in the writings of Gherardo of Cremona (c. 1114-87), who translated many of the Greek texts, including the Almagest, into Latin. Other writers followed, and soon the word sinus, or sine, was used in the mathematical literature throughout Europe. The abbreviated symbol sin was first used in 1624 by Edmund Gunter, an English minister and instrument maker. The notations for the five remaining trigonometric functions were introduced shortly thereafter. During the Middle Ages, while Europe was plunged into darkness, the torch of learning was kept alive by Arab and Jewish scholars living in Spain, Mesopotamia, and Persia. The first table of tangents and cotangents was constructed around 860 by H.abash al-H.āsib ("the Calculator"), who wrote on astronomy and astronomical instruments. Another Arab astronomer, al-Bā-ttā-in (c. 858-929), gave a rule for finding the elevation ø of the Sun above the horizon in terms of the length s of the shadow cast by a vertical gnomon of height h. Al-Bā-ttā-ni's rule, s = h sin (90° - ø)/sin ø, is equivalent to the formula s = h cot ø. Based on this rule he constructed a "table of shadows"—essentially a table of cotangents—for each degree from 1° to 90°. It was through al-Bā-ttā-ni's work that the Hindu half-chord function—equivalent to the modern sine—became known in Europe. Passage to Europe Until the 16th century it was chiefly spherical trigonometry that interested scholars—a consequence of the predominance of astronomy among the natural sciences. The first definition of a spherical triangle is contained in Book 1 of the Sphaerica, a three-book treatise by Menelaus of Alexandria (c. AD 100) in which Menelaus developed the spherical equivalents of Euclid's propositions for planar triangles. A spherical triangle was understood to mean a figure formed on the surface of a sphere by three arcs of great circles, that is, circles whose centres coincide with the centre of the sphere. There are several fundamental differences between planar and spherical triangles; for example, two spherical triangles whose angles are equal in pairs are congruent (identical in size as well as in shape), whereas they are only similar (identical in shape) for the planar case. Also, the sum of the angles of a spherical triangle is always greater than 180°, in contrast to the planar case where the angles always sum to exactly 180°. Several Arab scholars, notably Nas.īr al-Dīn al-T.ūsī (1201-74) and al-Bā-ttā-in, continued to develop spherical trigonometry and brought it to its present form. T.ūsī was the first (c. 1250) to write a work on trigonometry independently of astronomy. But the first modern book devoted entirely to trigonometry appeared in the Bavarian city of Nürnberg in 1533 under the title "On Triangles of Every Kind". Its author was the astronomer Regiomontanus (1436-76). On Triangles contains all the theorems needed to solve triangles, planar or spherical—although these theorems are expressed in verbal form, as symbolic algebra had yet to be invented. In particular, the law of sines (see the above table) is stated in essentially the modern way. On Triangles was greatly admired by future generations of scientists; the astronomer Nicolaus Copernicus (1473-1543) studied it thoroughly, and his annotated copy survives. The final major development in classical trigonometry was the invention of logarithms by the Scottish mathematician John Napier in 1614. His tables of logarithms greatly facilitated the art of numerical computation—including the compilation of trigonometry tables—and were hailed as one of the greatest contributions to science. Eli Maor, Ed.: Adjunct Professor of Mathematics, Loyola University, Chicago Illinois. Author of June 8, 2004: Venus in Transit; Trigonometric Delights and others.Source: "Trigonometry." Encyclopædia Britannica Ultimate Reference Suite, 2013. Trigonometric Table (A Trigonometric table displays) tabulated values for some or all of the six trigonometric functions for various angular values. Once an essential tool for scientists, engineers, surveyors, and navigators, trigonometry tables became obsolete with the availability of computers.  The Greek astronomer Hipparchus (d. c. 127 BC) was the first to compose a table of trigonometric functions (based on the chords in a circle), which he calculated at increments of 7° 30'. Ptolemy (d. c. AD 145) improved on Hipparchus's tables by calculating the values at 30' increments. Ptolemy's Almagest, the greatest astronomical work of antiquity, would be unimaginable without his table of chords. The earliest table of the sine function (although still not with its modern definition) is found in the Surya Siddhanta, a Hindu astronomical handbook from the 4th or 5th century AD. The astronomers of medieval Islam were consummate calculators who constructed tables of all six trigonometric functions as a basis for astronomy and astronomical timekeeping. The crown of this endeavour was Sultan Ulugh Beg's tables, published in 1440 in Samarkand (now in Uzbekistan). The sine and tangent functions (although still not given their modern definitions in terms of ratios), calculated at 1' increments, were accurate to the equivalent of 9 decimal places. From Muslim Spain, trigonometric tables spread to Latin Europe. Regiomontanus (1436-76), German astronomer and mathematician, composed the first tables with decimal values. Similarly, Georg Joachim Rheticus (1514-74), a student of Nicolaus Copernicus, prepared a magnificent set of tables of all six trigonometric functions at 10' increments accurate to 10 decimal places. Rheticus also took the decisive steps of defining the trigonometric functions in terms of angles rather than arcs and as ratios rather than lengths. The French mathematician François Viète published tables of all six trigonometric functions in Canon Mathematicus (1579). The value of this work was not, however, in the tables, in which he calculated the functions at 1' increments, accurate to five decimal places. Instead, Viète's work was important because he had discovered various trigonometry relationships with which he demonstrated how to use trigonometry to solve equations of degree three and higher. Henceforth, trigonometric tables were useful not only in surveying, astronomy, and navigation but in algebra as well. The climax for the construction of trigonometric tables in this period occurred with the German Bartholomeo Pitiscus. It was Pitiscus who coined the word trigonometry, and his Thesaurus Mathematicus (1615) contained tables of sines and cosines calculated at 10' intervals that were accurate to 15 decimal places. Later, still more accurate tables were constructed with the help of logarithms, invented by John Napier in 1614. Source: "Trigonometry Table." Encyclopædia Britannica Ultimate Reference Suite, 2013.Viète, François, Seigneur (lord) De La Bigotiere Latin: Franciscus Vietaborn 1540, Fontenay-le-Comte, France died Dec. 13, 1603, Paris (He was the) mathematician who introduced the first systematic algebraic notation and contributed to the theory of equations. Viète, a Huguenot sympathizer, solved a complex cipher of more than 500 characters used by King Philip II of Spain in his war to defend Roman Catholicism from the Huguenots. When Philip, assuming that the cipher could not be broken, discovered that the French were aware of his military plans, he complained to the pope that black magic was being employed against his country. Viète's "Canon mathematicus seu ad triangula" (1579; "Mathematical Laws Applied to Triangles") is probably the first western European work dealing with a systematic development of methods—utilizing all six trigonometric functions—for computing plane and spherical triangles. Viète has been called "the father of modern algebraic notation," and his "In artem analyticem isagoge" (1591; "Introduction to the Analytical Arts") closely resembles a modern elementary algebra text. His contribution to the theory of equations is "De aequationum recognitione et emendatione" (1615; "Concerning the Recognition and Emendation of Equations"), in which he presented methods for solving equations of second, third, and fourth degree. He knew the connection between the positive roots of an equation (which, in his time, were thought of as the only roots) and the coefficients of the different powers of the unknown quantity. "Viète, François, Seigneur (lord) De La Bigotiere." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
The following statement needs to be looked at a point of developmental departure in human cognition:
..."The value of this work was not, however, in the tables, in which he calculated the functions at 1' increments, accurate to five decimal places. Instead, Viète's work was important because he had discovered various trigonometry relationships with which he demonstrated how to use trigonometry to solve equations of degree three and higher."...
Solving equations two degrees and lower had now been surpassed. Similarly, if the Rosetta stone (as well as Galle Inscription or Behistun Rock formation) had displayed only two languages instead of three, later translations of works would have been all the more difficult... like having a genetic code which displayed only two amino acids. It is tantamount to replacing the old "many" label of the "one-two-many" primitive counting scheme, with the value "3". Even though the "three" cognitive pattern is retained in the compartmentalization of "ones - tens - hundreds"..., "thousands - ten-thousands - hundred-thousands,... etc...", the "three" had acquired its own distinctiveness as part of a group. The usage of the word "many" in the old counting system was, in a sense, a generic "tribe/clan" name of multiple (quantitative) entities and not an individuality. Likewise, whereas some may view the words "peace" and "war" as specifics, others note them as two faces of the same coin. War and peace do not have separate identity standards because is frequently used to acknowledge the other. Hence, we need a cognitive leap into a third realization which provides for actual separate distinctions.
Date of Origination: Friday, 14-April-2017... 04:16 AM
Date of initial posting: Tuesday, 25-April-2017... 11:30 AM Updated posting: Saturday, 31-March-2018... 12:59 PM